ΜΕΜ-112 Εισαγωγή στη Γραμμική Άλγεβρα (Χειμερινό 2020)
Section outline
-

Διδάσκοντες
Θεόδουλος Γαρεφαλάκης (Τμήμα Α)
Γραφείο : Γ216 email : tgaref@uoc.gr Σύγχρονη διδασκαλία : Τρίτη 11-1 (Zoom link) Γιώργος Καπετανάκης (Τμήμα Β)
Γραφείο : Γ212 email : gnkapet@gmail.com Σύγχρονη διδασκαλία : Δευτέρα 11-1 (Zoom link, ID: 727 6942 1258, passcode: 0Pteuy) Βοηθοί
- Ευαγγελία Καρτσάκη (mathp397@math.uoc.gr)
- Σοφία Παντελάκη (mathp379@math.uoc.gr)
- Χρυσαφίνα Ροδίτου (mathp390@math.uoc.gr)
- Νίκη Σπιθάκη (mathp393@math.uoc.gr)
Πρόγραμμα Εργαστηρίων
- Σοφία Παντελάκη: Πέμπτη 11.00-13.00 (Zoom link, ID: 959 056 1472, Passcode: d9gDp9)
- Χρυσαφίνα Ροδίτου: Παρασκευή 9.00-11.00 (Zoom link, ID: 750 8722 1594, Passcode: mu2b1Y)
- Νίκη Σπιθάκη: Παρασκευή 11.00-13.00 (Zoom link, ID: 750 2225 7490, Passcode: 3333 Κωδικός ομάδας MS-Teams: mgzv036)
- Ευαγγελία Καρτσάκη: Παρασκευή 11.00-13.00 (Zoom link, ID: 771 6529 3517, Passcode: P0VSEs)
Συγγράμματα
- Οι σημειώσεις του κ. Κουρουνιώτη.
- Μια εισαγωγή στην Γραμμική Άλγεβρα, Βάρσος, Δεριζιώτης Εμμανουήλ,Μαλιάκας, Μελάς, Ταλλέλη.
- Μια εισαγωγή στη Γραμμική Άλγεβρα, Χαραλάμπους, Φωτιάδης.
- Γραμμική Άλγεβρα και εφαρμογές, G. Strang.
- Γραμμική Άλγεβρα, Θεοχάρη-Αποστολίδη, Βαβατσούλας, Χαραλάμπους.
- Μια εισαγωγή στην Γραμμική Άλγεβρα, A. Morris.
Διδασκαλία
Η διδασκαλία του μαθήματος θα γίνει με ασχύγχρονο τρόπο. Θα αναρτούμε στην ιστοσελίδα του μαθήματος, ανά εβδομάδα, βιντεοσκοπημένες διαλέξεις, διαφάνειες και οδηγίες για μελέτη από τη προτεινόμενη βιβλιογραφία. Επίσης, θα αναρτούμε φυλλάδια ασκήσεων, πάνω στα οποία πρέπει να δουλεύετε. Είναι σημαντικό να προσπαθείτε να λύνετε τις ασκήσεις μόνοι σας. Θα αναρτούμε λύσεις επιλεγμένων ασκήσεων μερικές εβδομάδες μετά την ανακοίνωση κάθε φυλλαδίου ασκήσεων. Μπορείτε να επικοινωνείτε μαζί μας μέσω ηλεκτρονικού ταχυδρομείου, μέσω του forum του μαθήματος ή στις ώρες γραφείου που θα ανακοινωθούν σύντομα. Οι ώρες γραφείου θα γίνονται μέσω κάποιας πλατφόρμας τηλεδιάσκεψης.
Βαθμολογία
Το μάθημα θα έχει δύο προόδους, ένα τελικό διαγώνισμα και προφορική εξέταση. Οι δύο πρόοδοι θα γίνουν εξ αποστάσεως, μέσω της ιστοσελίδας του μαθήματος. Για να περάσετε το μάθημα πρέπει να φτάσετε και να επιτύχετε στην προφορική εξέταση. Για να φτάσετε στη προφορική εξέταση πρέπει να γράψετε βαθμό τουλάχιστον 3/10 σε κάθε μία από τις προόδους και στο τελικό διαγώνισμα και πρέπει ο μέσος όρος των βαθμών των τριών εξετάσεων να είναι τουλάχιστον 5/10. Ο τελικός σας βαθμός καθορίζεται από την προφορική εξέταση. Για τη συμμετοχή σας στην εξέταση του Σεπτεμβρίου θα πρέπει να έχετε γράψει τουλάχιστον 3 σε κάθε μία από τις δύο προόδους.
Η πρώτη πρόοδος θα γίνει το Σάββατο 7 Νοεμβρίου στις 11:00 Σάββατο 14 Νοεμβρίου στις 11:00.
Η δεύτερη πρόοδος θα γίνει το Σάββατο 5 Δεκεμβρίου στις 11:00.
Το τελικό διαγώνισμα θα γίνει σύμφωνα με το πρόγραμμα της εξεταστικής περιόδου του Ιανουαρίου, όπως θα ανακοινωθεί από το Τμήμα.
Το τελικό διαγώνισμα θα γίνει την Παρασκευή 29 Ιανουαρίου. Τουλάχιστον μία ημέρα νωρίτερα, θα εμφανιστεί στην ιστοσελίδα του μαθήματος ο σύνδεσμος για το διαγώνισμα. Στις 9:00 το πρωί (της Παρασκευής 29/1) θα "ανοίξει" το διαγώνισμα. Η μορφή του διαγωνίσματος (και η διάρκεια του) θα είναι παρόμοια με αυτή των δύο προηγούμενων διαγωνισμάτων.
Μέχρι αύριο (Σάββατο 30/1) θα ανακοινωθεί στην ιστοσελίδα του μαθήματος το πρόγραμμα των προφορικών εξετάσεων. Σε προφορική εξέταση θα προχωρήσουν όσες/όσοι έχουν άθροισμα βαθμών των τριών διαγωνισμάτων τουλάχστον 14.50 14.25 (μέσο όρο 4.75). Η προφορική εξέταση θα γίνει μέσω της πλατφόρμας zoom και θα πρέπει να έχετε ανοιχτά μικρόφωνο και κάμερα. Επίσης, χρειάζεστε μία ταυτότητα για ταυτοποίηση στοιχείων καθώς και χαρτί/μολύβι.
Το πρόγραμμα των προφορικών εξετάσεων φαίνεται στις δύο παρακάτω λίστες. Η 1η λίστα περιέχει φοιτητές/τριες που το επώνυμο τους αρχίζει από Α-Λ. Η 2η λίστα περιέχει φοιτητές/τριες που το επώνυμο τους αρχίζει από Μ-Ω. Για να συμμετάσχετε στην εξέταση, συνδεθείτε την προγραμματισμένη ώρα, μέσω της πλατφόρμας zoom, ακολουθώντας τον αντίστοιχο σύνδεσμο.
Α - Λ : λίστα συμμετεχόντων (zoom: https://us02web.zoom.us/j/82170516592)
Μ - Ω: λίστα συμμετεχόντων (zoom: https://us04web.zoom.us/j/72526712463?pwd=dEp1dXhma3QxcDAwdFcwUjF6RDZwdz09)
Η εξέταση του μαθήματος στην εξεταστική περίοδο του Σεπτεμβρίου, θα πραγματοποιηθεί εξ' αποστάσεως, με τον ίδιο τρόπο που έγινε και στην εξεταστική περίοδο του Ιανουαρίου. Η ώρα της εξέτασης θα είναι αυτή που θα ανακοινωθεί στο πρόγραμμα των εξετάσεων. Η διάρκεια και η μορφή του διαγωνίσματος θα είναι παρόμοια με αυτή των προηγούμενων διαγωνισμάτων. Ο σύνδεσμός για το διαγώνισμα θα εμφανιστεί σε αυτή την ιστοσελίδα, μία τουλάχιστον ημέρα νωρίτερα. Μετά το τέλος της εξέτασης (ενδεχομένως μερικές μέρες μετά), θα ανακοινωθούν οι ΑΜ των φοιτητών/τριών που πρέπει να προσέλθουν σε προφορική εξέταση. Λεπτομέρειες για την προφορική εξέταση θα δοθούν τότε.
Η εξέταση του μαθήματος στην εξεταστική περίοδο του Σεπτεμβρίου θα γίνει την Δευτέρα 23/08, το κουίζ θα ανοίξει στις 9.00 το πρωί και η εξέταση θα έχει διάρκεια 90 λεπτά. Μετά το τέλος της εξέτασης (ενδεχομένως μερικές μέρες μετά), θα ανακοινωθούν οι ΑΜ των φοιτητών/τριών που πρέπει να προσέλθουν σε προφορική εξέταση. Λεπτομέρειες για την προφορική εξέταση θα δοθούν τότε.
Το πρόγραμμα των προφορικών εξετάσεων για τα δύο τμήματα φαίνεται παρακάτω.
Α - Λ: Λίστα συμμετεχόντων (zoom: https://us02web.zoom.us/j/8128230266?pwd=ZUlVWUMycDJpSWhuRkpnWGVucnBxZz09)
Μ - Ω: Λίστα συμμετεχόντων (zoom: https://us04web.zoom.us/j/74445143398?pwd=blpRNHE4WFcrby9WcytlVHNGUlg2QT09)
-
Αρχίσαμε το μάθημα με τη μελέτη γραμμικών συστημάτων. Παρακάτω θα βρείτε τα video των διαλέξεων και τις σχετικές διαφάνειες. Μπορείτε να μελετήσετε από το σύγγραμμα [3] (στη λίστα παραπάνω), τις παραγράφους 1.1, 1.2 και 1.3. Επίσης, δείτε από το σύγγραμμα [1] τις παραγράφους από 2.1 έως και 2.4.
Αναρτήθηκε το 1ο φυλλάδιο ασκήσεων (δείτε παραπάνω).
-
Συνεχίζουμε με τις έννοιες του (αριθμητικού) διανύσματος και του πίνακα. Δείτε τις παρακάτω διαλέξεις στις οποίες ορίζουμε το χώρο
 και δύο πράξεις: πρόσθεση διανυσμάτων και βαθμωτό πολλαπλασιασμό αριθμού με διάνυσμα. Στη συνέχεια ορίζουμε το χώρο
και δύο πράξεις: πρόσθεση διανυσμάτων και βαθμωτό πολλαπλασιασμό αριθμού με διάνυσμα. Στη συνέχεια ορίζουμε το χώρο 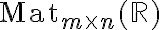 των
των 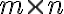 πινάκων και ορίζουμε τρεις πράξεις: πρόσθεση πινάκων, βαθμωτό πολλαπλασιασμό αριθμού με πίνακα και πολλαπλασιασμό πινάκων. Μελετήστε την παράγραφο 2.1 από το σύγγραμμα [3] και τις παραγράφους 1.6, 2.2, 2.5 από το σύγγραμμα [1].
πινάκων και ορίζουμε τρεις πράξεις: πρόσθεση πινάκων, βαθμωτό πολλαπλασιασμό αριθμού με πίνακα και πολλαπλασιασμό πινάκων. Μελετήστε την παράγραφο 2.1 από το σύγγραμμα [3] και τις παραγράφους 1.6, 2.2, 2.5 από το σύγγραμμα [1].Αναρτήθηκε το 2ο φυλλάδιο ασκήσεων.
-
Ορίσαμε τον μοναδιαίο πίνακα
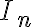 και είδαμε τις βασικές ιδιότητές του. Μετά συνεχίσαμε με τον ορισμό του αντιστρέψιμου πίνακα και του αντίστροφου ενός αντιστρέψιμου πίνακα, ενώ αποδείξαμε ότι ο αντίστροφος (αν υπάρχει) είναι μοναδικός, ενώ είδαμε και μερικες επιπλέον βασικές ιδιότητες της αντιστροφής πινάκων. Ακόμα περιγράψαμε την μέθοδο Gauss-Jordan για την εύρεση του αντίστροφου. Στη συνέχεια, ορίσαμε τον ανάστροφο ενός πίνακα, είδαμε τις βασικές ιδιότητες του μετασχηματισμού αυτού, ενώ είδαμε τις έννοιες της συμμετρίας και της αντισυμμετρίας πινάκων. Τέλος, ορίσαμε τους στοιχειώδεις πίνακες (πίνακες διάτμησης, πολλαπλασιασμού, εναλλαγής και μετάθεσης) και είδαμε την αντιστοιχία με τις πράξεις γραμμών. Μελετήστε τις παραγράφους 2.7, 2.8 και 3.4 του συγγράματος [1].
και είδαμε τις βασικές ιδιότητές του. Μετά συνεχίσαμε με τον ορισμό του αντιστρέψιμου πίνακα και του αντίστροφου ενός αντιστρέψιμου πίνακα, ενώ αποδείξαμε ότι ο αντίστροφος (αν υπάρχει) είναι μοναδικός, ενώ είδαμε και μερικες επιπλέον βασικές ιδιότητες της αντιστροφής πινάκων. Ακόμα περιγράψαμε την μέθοδο Gauss-Jordan για την εύρεση του αντίστροφου. Στη συνέχεια, ορίσαμε τον ανάστροφο ενός πίνακα, είδαμε τις βασικές ιδιότητες του μετασχηματισμού αυτού, ενώ είδαμε τις έννοιες της συμμετρίας και της αντισυμμετρίας πινάκων. Τέλος, ορίσαμε τους στοιχειώδεις πίνακες (πίνακες διάτμησης, πολλαπλασιασμού, εναλλαγής και μετάθεσης) και είδαμε την αντιστοιχία με τις πράξεις γραμμών. Μελετήστε τις παραγράφους 2.7, 2.8 και 3.4 του συγγράματος [1].Αναρτήθηκε το 3ο φυλλάδιο ασκήσεων.
-
Είδαμε ότι οι αντίστροφοι των στοιχειωδών πινάκων είναι στοιχειώδης πίνακες και ότι το γινόμενο άνω, κάτω ή διαγώνιων πινάκων είναι της ίδιας μορφής. Μετά είδαμε την απαλοιφή Gauss μέσω πινάκων και οδηγηθήκαμε στην ανάλυση LU και την γενίκευσή της σε πίνακες που δεν έχουν τέτοια ανάλυση. Έπειτα ορίσαμε τους ιδιόμορφους πίνακες και ασχοληθήκαμε με ομογενή και μη ομογενή συστήματα, Κλείσαμε με τον ορισμό της τάξης ενός πίνακα. Μελετήστε τις παραγράφους 3.1, 3.2, 3.3, 4.3, 4.4 και 4.5 του συγγράματος [1].
Αναρτήθηκε το 4ο φυλλάδιο ασκήσεων.
-
Ορίσαμε την έννοια του διανυσματικού ή γραμμικού χώρου και είδαμε κάποιες βασικές ιδιότητες. Είδαμε την έννοια του υπόχωρου ενός διανυσματικού χώρου, ο οποίος είναι διανυσματικός χώρος με πράξεις τους περιορισμους των πράξεων του αρχικού χώρου. Ορίσαμε την έννοια του γραμμικού συνδυασμού διανυσμάτων και της γραμμικής θήκης ενός συνόλου διανυσμάτων. Χαρακτηρίσαμε τη γραμμική θήκη ενός συνόλου
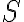 ως το σύνολο των γραμμικών συνδυσμών διανυσμάτων του
ως το σύνολο των γραμμικών συνδυσμών διανυσμάτων του 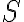 . Αποδείξαμε κάποιες βασικές προτάσεις. Το υλικό αυτό αντιστοιχεί στις παραγράφους 5.1 έως 5.6 του συγγράμματος [1].
. Αποδείξαμε κάποιες βασικές προτάσεις. Το υλικό αυτό αντιστοιχεί στις παραγράφους 5.1 έως 5.6 του συγγράμματος [1].Αναρτήθηκε το 5ο φυλλάδιο ασκήσεων.
-
Βλέπουμε μία νέα κατασκεύη ενός υπόχωρου από δεδομένους υπόχωορυς: το άθροισμα τους. Επίσης, ορίζουμε πότε το άθροισμα υποχώρων είναι ευθύ. Δείτε την παράγραφο 5.7 του [1]. Στη συνέχεια ορίζουμε την έννοια της γραμμικής εξάρτησης και της γραμμικής ανεξαρτησίας ενός συνόλου διανυσμάτων. Δίνουμε παραδείγματα και τα πρώτα αποτελέσματα. Δείτε τις παραγράφους 6.1 και 6.2 από το [1], μέχρι (και χωρίς) το Θεώρημα Αντικατάστασης.
Αναρτήθηκε το 6ο φυλλάδιο ασκήσεων.
-
Βλέπουμε το Θεώρημα Αντικατάστασης και κάποιες βασικές συνέπειες του. Βλέπουμε τον ορισμό της έννοιας της βάσης και τα πρώτα πραδείγματα. Μελετήσαμε την έννοια της βάσης. Είδαμε την έννοια της διάστασης. Στο χρονικό σημείο 7:25 του 1ου βίντεο αναφέρουμε, λανθασμένα, ότι
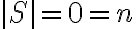 . Το σωστό είναι
. Το σωστό είναι 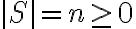 . Στο χρονικό σημείο 8:50 του 2ου βίντεο αντικαταστήστε το
. Στο χρονικό σημείο 8:50 του 2ου βίντεο αντικαταστήστε το 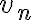 στο πρώτο άθροισμα με
στο πρώτο άθροισμα με 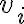 . Μπορείτε να διαβάσετε τις παραγράφους 6.2, 6.3, 6.4 και 6.7 από το σύγγραμμα [1].
. Μπορείτε να διαβάσετε τις παραγράφους 6.2, 6.3, 6.4 και 6.7 από το σύγγραμμα [1].Αναρτήθηκε το 7ο φυλλάδιο ασκήσεων.
-
Ορίσαμε και μελετήσαμε τους τέσσερις θεμελιώδεις υπόχωρους σχετιζόμενους με έναν πίνακα
 , τον χώρο στηλών, τον χώρο γραμμών, τον μηδενόχωρο και τον αριστερό μηδενόχωρο. Είδαμε την διάσταση ενός υπόχωρου ενός διανυσματικού χώρου πεπερασμένης διάστασης, την διάσταση του αθροίσματων υπόχωρων πεπερασμένης διάστασης, ορίσαμε τον συμπληρωματικό υπόχωρο και είδαμε ότι ο χώρος γραμμών και ο μηδενόχωρος ενός πίνακα είναι συμπληρωματικοί ο ένας του άλλου.
, τον χώρο στηλών, τον χώρο γραμμών, τον μηδενόχωρο και τον αριστερό μηδενόχωρο. Είδαμε την διάσταση ενός υπόχωρου ενός διανυσματικού χώρου πεπερασμένης διάστασης, την διάσταση του αθροίσματων υπόχωρων πεπερασμένης διάστασης, ορίσαμε τον συμπληρωματικό υπόχωρο και είδαμε ότι ο χώρος γραμμών και ο μηδενόχωρος ενός πίνακα είναι συμπληρωματικοί ο ένας του άλλου.Αναρτήθηκε το 8ο φυλλάδιο ασκήσεων.
Μελετήστε τις παραγράφους 6.5 και 6.6 του συγγράμματος [1].
-
Έγινε μια εισαγωγή στον χώρο των γραμμικών απεικονίσεων. Είδαμε τον ορισμό και τον χαρακτηρισμό μιας γραμμικής απεικόνισης
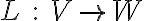 και τις αντίστοιχες βασικές προτάσεις και ιδιότητες, είδαμε παραδείγματα γραμμικών απεικονίσεων, είδαμε μια αντιστοιχία ανάμεσα στους
και τις αντίστοιχες βασικές προτάσεις και ιδιότητες, είδαμε παραδείγματα γραμμικών απεικονίσεων, είδαμε μια αντιστοιχία ανάμεσα στους 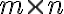 πραγματικούς πίνακες και τις γραμμικές απεικονίσεις
πραγματικούς πίνακες και τις γραμμικές απεικονίσεις 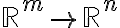 . Στην συνέχεια ορίσαμε τον πυρήνα και την εικόνα μιας γραμμικής απεικόνισης, δείξαμε ότι πρόκειται για υπόχωρους και δείξαμε ότι αν
. Στην συνέχεια ορίσαμε τον πυρήνα και την εικόνα μιας γραμμικής απεικόνισης, δείξαμε ότι πρόκειται για υπόχωρους και δείξαμε ότι αν 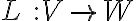 , τότε
, τότε 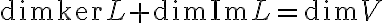 . Τέλος, δείξαμε ότι κάθε γραμμική απεικόνιση
. Τέλος, δείξαμε ότι κάθε γραμμική απεικόνιση 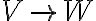 χαρακτηρίζεται πλήρως από την απεικόνιση των στοιχείων μιας βάσης του
χαρακτηρίζεται πλήρως από την απεικόνιση των στοιχείων μιας βάσης του  .
.Αναρτήθηκε το 9ο φυλλάδιο ασκήσεων.
Μελετήστε την παράγραφο 7.1 από το σύγγραμμα [1].
-
-
Ορίσαμε τις έννοιες του μονομορφισμού, του επιμορφισμού και του ισομορφισμού, καθώς και εκείνη των ισόμορφων διανυσματικών χώρων. Είδαμε κάποια αποτελέσματα που μας επιτρέπουν τον χαρακτηρισμό τέτοιων γραμμικών απεικονίσεων, καθώς και την έννοια της αντίστροφης και αντιστρέψιμης γραμμικής απεικόνισης. Δείξαμε ότι η ισομορφία διανυσματικών χώρων είναι συμμετρική, ανακλαστική και μεταβατική και, μέσω του διανύσματος συντεταγμένων, δείξαμε ότι κάθε διανυσματικός χώρος διάστασης
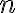 είναι ισόμορφος με τον
είναι ισόμορφος με τον  . Τέλος, ως αποτέλεσμα των αποτελεσμάτων αυτών, πήραμε ότι αν
. Τέλος, ως αποτέλεσμα των αποτελεσμάτων αυτών, πήραμε ότι αν 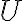 και
και  πεπερασμένα παραγόμενοι χώροι, τότε
πεπερασμένα παραγόμενοι χώροι, τότε 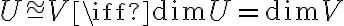 . Μελετήστε τις παραγράφους 7.3 και 7.4 του συγγράμματος [1] και την παράγραφο 5.1 του συγγράμματος [2].
. Μελετήστε τις παραγράφους 7.3 και 7.4 του συγγράμματος [1] και την παράγραφο 5.1 του συγγράμματος [2].Αναρτήθηκε το 10ο φυλλάδιο ασκήσεων.
-
Είδαμε πώς μπορούμε να χρησιμοποιούμε την απεικόνιση συντεταγμένων για να "μεταφέρουμε" το πρόβλημα μας από το δοσμένο χώρο
 στο χώρο
στο χώρο  , όπου
, όπου 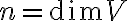 . Ορίσαμε τον πίνακα μία γραμμικής απεικόνισης
. Ορίσαμε τον πίνακα μία γραμμικής απεικόνισης 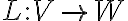 ως προς βάσεις
ως προς βάσεις 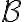 και
και 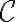 των χώρων
των χώρων 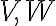 αντίστοιχα. Είδαμε πώς να τον χρησιμοποιούμε για να υπολογίζουμε τιμές της
αντίστοιχα. Είδαμε πώς να τον χρησιμοποιούμε για να υπολογίζουμε τιμές της 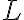 και να αποδεικνύουμε προτάσεις. Αποδείξαμε ότι οι χώροι
και να αποδεικνύουμε προτάσεις. Αποδείξαμε ότι οι χώροι 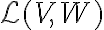 και
και 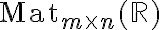 είναι ισόμορφοι. Ορίσαμε την έννοια του δυϊκού χώρου, ενός χώρου
είναι ισόμορφοι. Ορίσαμε την έννοια του δυϊκού χώρου, ενός χώρου  και τη δϋική βάση μίας βάσης του
και τη δϋική βάση μίας βάσης του  . Μπορείτε να διαβάσετε την παράγραφο 8.1 του συγγράμματος [1].
. Μπορείτε να διαβάσετε την παράγραφο 8.1 του συγγράμματος [1].Αναρτήθηκε το 11ο φυλλάδιο ασκήσεων.
-
Είδαμε ότι ο πίνακας της σύνθεσης δύο γραμμικών απεικονίσεων είναι το γινόμενο των πινάκων των απεικονίσεων αυτών και ορίσαμε τον πίνακα αλλαγής βάσης . Τέλος, χρησιμοποιώντας τα παραπάνω, δείξαμε ποιά είναι η σύνδεση ανάμεσα στους πίνακες
![[L]_{\mathcal{B}}^{\mathcal{C}} [L]_{\mathcal{B}}^{\mathcal{C}}](https://elearn.uoc.gr/filter/tex/pix.php/4442ebb3e4d9a2f3e164760f9743bd20.gif) και
και ![[L]_{\mathcal{B'}}^{\mathcal{C'}} [L]_{\mathcal{B'}}^{\mathcal{C'}}](https://elearn.uoc.gr/filter/tex/pix.php/733aa974f6a1bb04438aa5ab6c3b5c2b.gif) , όπου
, όπου 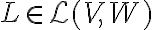 και
και 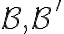 δύο βάσεις του
δύο βάσεις του  και
και 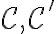 δύο βάσεις του
δύο βάσεις του 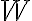 . Μελετήστε τις παραγράφους 8.2 και 8.3 του συγγράμματος [1].
. Μελετήστε τις παραγράφους 8.2 και 8.3 του συγγράμματος [1].Αναρτήθηκε το 12ο φυλλάδιο ασκήσεων.

