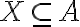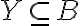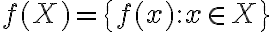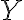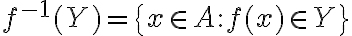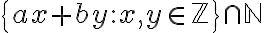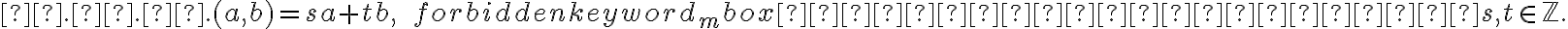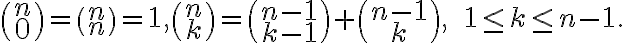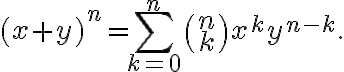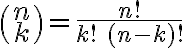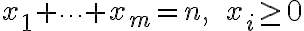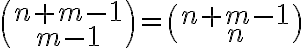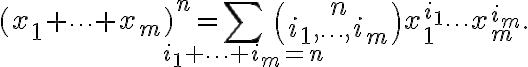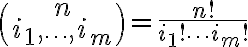ΜΕΜ-103 Θεμέλια των Μαθηματικών (Εαρινό 2025)
Section outline
-

Διδάσκων
Θεόδουλος Γαρεφαλάκης
Γραφείο Γ216 email tgaref@uoc.gr Ώρες γραφείου Τρίτη 11:00 - 13:00 Διαλέξεις
Τρίτη 9:00 - 11:00 (Α201) Πέμπτη 9:00 - 11:00 (Α201) Εργαστήριο
Παρασκευή 13:00 - 15:00 (Ε212) Φροντιστήριο
Δευτέρα 13:00 - 15:00 (Α212) Βαθμολογικό Σύστημα
Θα γίνει μία πρόοδος περίπου στα μέσα του εξαμήνου και μία τελική εξέταση στην εξεταστική περίοδο του Ιουνίου. Εάν ο βαθμός της προόδου είναι
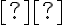 και ο βαθμός της τελικής εξέτασης είναι
και ο βαθμός της τελικής εξέτασης είναι 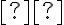 , τότε ο βαθμός του μαθήματος υπολογίζεται ως
, τότε ο βαθμός του μαθήματος υπολογίζεται ως 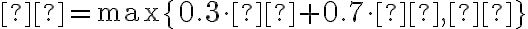 . Ο βαθμός της προόδου δεν μετράει στην εξέταση του Σεπτεμβρίου (εφόσον χρειαστεί να εξεταστείτε το Σεπτέμβρη). Σε κάθε φυλλάδιο ασκήσεων (από το 2ο φυλλάδιο και έπειτα), αναφέρονται κάποιες ασκήσεις προς παράδωση. Μπορείτε να δίνεται τις ασκήσεις αυτές κατά τη διάρκεια του εργαστηρίου. Οι ασκήσεις αυτές δίνουν έως μία μονάδα επιπλέον στον τελικό βαθμό σας (και ανάλογα με το πόσες ασκήσεις θα παραδώσετε κατά τη διάρκεια του εξαμήνου: αν για παράδειγμα, παραδώσετε τις μισές ασκήσεις, θα πάρετε μισή μονάδα).
. Ο βαθμός της προόδου δεν μετράει στην εξέταση του Σεπτεμβρίου (εφόσον χρειαστεί να εξεταστείτε το Σεπτέμβρη). Σε κάθε φυλλάδιο ασκήσεων (από το 2ο φυλλάδιο και έπειτα), αναφέρονται κάποιες ασκήσεις προς παράδωση. Μπορείτε να δίνεται τις ασκήσεις αυτές κατά τη διάρκεια του εργαστηρίου. Οι ασκήσεις αυτές δίνουν έως μία μονάδα επιπλέον στον τελικό βαθμό σας (και ανάλογα με το πόσες ασκήσεις θα παραδώσετε κατά τη διάρκεια του εξαμήνου: αν για παράδειγμα, παραδώσετε τις μισές ασκήσεις, θα πάρετε μισή μονάδα).Συγγράμματα
- Σημειώσεις του μαθήματος "Θεμέλια των Μαθηματικών", Χ. Κουρουνιώτης
- Αφελής Συνολοθεωρία, P. Halmos, Εκκρεμές.
- Σύνολα και Αριθμοί: Μία εισαγωγή στα Μαθηματικά, Τσολομύτης, LEADER BOOKS
- The Foundations of Mathematics, Stewart and Tall, Oxford University Press.
Συνιστούμε ισχυρά να παρακολουθείτε τις διαλέξεις και να συμμετέχετε στα εργαστήρια. Λύνοντας ασκήσεις στην διάρκεια του εξαμήνου είναι ο καλύτερος τρόπος αφενός να μάθετε και αφετέρου να εξασκηθείτε για τις εξετάσεις του μαθήματος.
-
Κάναμε μία εισαγωγή στην έννοια του συνόλου. Μιλήσαμε για υποσύνολα και είδαμε ότι δύο σύνολα
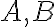 είναι ίσα αν και μόνο αν
είναι ίσα αν και μόνο αν 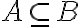 και
και 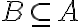 . Χρησιμοποιήσαμε αυτή τη βασική πρόταση για να δείξουμε διάφορες ισότητες συνόλων στη συνέχεια.
. Χρησιμοποιήσαμε αυτή τη βασική πρόταση για να δείξουμε διάφορες ισότητες συνόλων στη συνέχεια.Ορίσαμε την έννοια της ένωσης και της τομής συνόλων και δείξαμε κάποιες (απλές) προτάσεις.
Ορίσαμε τη διαφορά συνόλων και το συμπλήρωμα ενός συνόλου εντός ενός υπερσυνόλου (που συχνά ονομάζουμε σύμπαν). Δείξαμε τους κανόνες De Morgan. Ορίσαμε τη συμμετρική διαφορά δύο συνόλων.
Ορίσαμε άπειρες ενώσεις και τομές συνόλων και είδαμε παραδείγματα.
Διαβάστε: σελ. 1-9 από τις σημειώσεις Χ. Κουρουνιώτη.
Διαβάστε: σελ. 9-16 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Ορίσαμε το καρτεσιανό γινόμενο δύο συνόλων
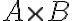 και είδαμε παραδείγματα και βασικές ιδιότητες.
και είδαμε παραδείγματα και βασικές ιδιότητες. Ορίσαμε μία σχέση
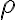 μεταξύ των συνόλων
μεταξύ των συνόλων 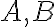 , ως ένα υποσύνολο του
, ως ένα υποσύνολο του 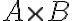 . Είδαμε παραδείγματα σχέσεων.
. Είδαμε παραδείγματα σχέσεων.Ονομάσαμε μία σχέση
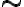 επί ενός συνόλου
επί ενός συνόλου  , σχέση ισοδυναμίας, όταν είναι ανακλαστική, συμμετρική και μεταβατική.
, σχέση ισοδυναμίας, όταν είναι ανακλαστική, συμμετρική και μεταβατική. Είδαμε ότι για ένα μην μηδενικό
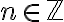 , μπορούμε να ορίσουμε στο
, μπορούμε να ορίσουμε στο 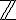 τη σχέση
τη σχέσηΗ παραπάνω σχέση είναι σχέση ισοδυναμίας.
Διαβάστε: σελ. 17-24 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Δεδομένης μίας σχέσης ισοδυναμίας
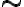 σε ένα σύνολο
σε ένα σύνολο 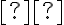 , ορίσαμε την κλάση του στοιχείου
, ορίσαμε την κλάση του στοιχείου  ως το σύνολο των στοιχείων του
ως το σύνολο των στοιχείων του  που είναι ισοδύναμα με το
που είναι ισοδύναμα με το 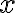
Συμβολίσαμε το σύνολο όλων των κλάσεων της σχέσης
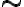 με
με Μελετήσαμε τη σχέση
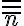 (ορισμένη στο
(ορισμένη στο 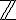 για ένα σταθεροποιημένο μη μηδενικό
για ένα σταθεροποιημένο μη μηδενικό 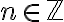 ),
),Δείξαμε ότι
και ότι όλες οι παραπάνω κλάσεις είναι ανά δύο διαφορετικές.
Είδαμε ότι οι κλάσεις ισοδυναμίας ορίζουν μία διαμέριση του συνόλου και αντίστροφα: κάθε διαμέριση του συνόλου
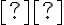 ορίζει μία σχέση ισοδυναμίας.
ορίζει μία σχέση ισοδυναμίας.Ορίσαμε την έννοια της σχέσης διάταξης και είδαμε παραδείγματα.
Σε ένα σύνολο
 , στο οποίο έχουμε ορίσει μία σχέση διάταξης, ορίσαμε την έννοια του μεγιστικού και την έννοια του μέγιστου στοιχείου. Είδαμε ότι μπορεί να υπάρχουν πολλά μεγιστικά στοιχεία. Όταν υπάρχει μέγιστο στοιχείο, αυτό είναι μοναδικό και είναι το μοναδικό μεγιστικό στοιχείο του
, στο οποίο έχουμε ορίσει μία σχέση διάταξης, ορίσαμε την έννοια του μεγιστικού και την έννοια του μέγιστου στοιχείου. Είδαμε ότι μπορεί να υπάρχουν πολλά μεγιστικά στοιχεία. Όταν υπάρχει μέγιστο στοιχείο, αυτό είναι μοναδικό και είναι το μοναδικό μεγιστικό στοιχείο του  (πάντα ως προς τη σχέση διάταξης την οποία μελατάμε).
(πάντα ως προς τη σχέση διάταξης την οποία μελατάμε).Ορίσαμε την έννοια της συνάρτησης
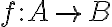 , με πεδίο ορισμού
, με πεδίο ορισμού  και πεδίο τιμών
και πεδίο τιμών 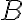 .
. Ορίσαμε πότε μία συνάρτηση είναι ένα-προς-ένα και πότε είναι επί.
Ορίσαμε τη σύθεση συναρτήσεων και την έννοια της αντίστροφης συνάρτησης, μίας δεδομένης συνάρτησης
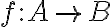 .
.Διαβάστε: σελ. 24-31 από τις σημειώσεις Χ. Κουρουνιώτη.
Διαβάστε: σελ. 32-49 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Μελετήσαμε τις έννοιες του αριστερού/δεξιού αντιστρόφου μίας συνάρτησης
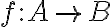 .
.Δείξαμε ότι
- η συνάρτηση
 έχει αριστερό αντίστροφο αν και μόνο αν είναι 1-1.
έχει αριστερό αντίστροφο αν και μόνο αν είναι 1-1. - η συνάρτηση
 έχει δεξιό αντίστροφο αν και μόνο αν είναι επί.
έχει δεξιό αντίστροφο αν και μόνο αν είναι επί.
Δείξαμε ότι η
 είναι αντιστρέψιμη αν και μόνο αν είναι 1-1 και επί. Σε αυτή την περίπτωση η αντίστροφη συνάρτηση είναι μοναδική και συμβολίζεται
είναι αντιστρέψιμη αν και μόνο αν είναι 1-1 και επί. Σε αυτή την περίπτωση η αντίστροφη συνάρτηση είναι μοναδική και συμβολίζεται 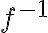 .
. Ονομάσαμε την εικόνα του συνόλου
 , εικόνα της συνάρτησης
, εικόνα της συνάρτησης  και τη συμβολίσαμε με
και τη συμβολίσαμε με 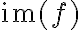 . Με άλλα λόγια,
. Με άλλα λόγια, 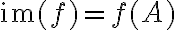 .
.Διαβάστε: σελ. 49-53 από τις σημειώσεις Χ. Κουρουνιώτη.
- η συνάρτηση
-
Για
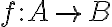 και
και 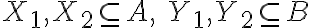 , αποδείξαμε κάποιες βασικές ιδιότητες για τα
, αποδείξαμε κάποιες βασικές ιδιότητες για τα 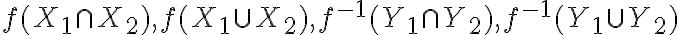 .
.Μιλήσαμε για τον περιορισμό μίας συνάρτησης σε ένα υποσύνολο του πεδίου ορισμού της.
Μιλήσαμε για (διμελείς) πράξεις σε ένα σύνολο
 . Ορίσαμε πότε μία πράξη ονομάζεται μεταθετική και πότε προσεταιριστική. Είδαμε παραδείγματα.
. Ορίσαμε πότε μία πράξη ονομάζεται μεταθετική και πότε προσεταιριστική. Είδαμε παραδείγματα. Διαβάστε: σελ. 54-58 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Κάναμε μία εισαγωγή στην Προτασιακή Λογική. Μιλήσαμε για σύνταξη τύπων και δώσαμε έννοια στους συνδέσμους
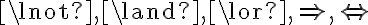 , ορίζοντας τον πίνακα αληθείας για κάθε ένα. Είδαμε ότι με αυτούς τους ορισμούς, μπορεί να αποδοθεί μία τιμή αληθείας σε κάθε τύπο, όταν δοθούν τιμές αληθείας στις προτασιακές μεταβλητές: μπορούμε δηλαδή να φτιάξουμε τον πίνακα αληθείας του τύπου.
, ορίζοντας τον πίνακα αληθείας για κάθε ένα. Είδαμε ότι με αυτούς τους ορισμούς, μπορεί να αποδοθεί μία τιμή αληθείας σε κάθε τύπο, όταν δοθούν τιμές αληθείας στις προτασιακές μεταβλητές: μπορούμε δηλαδή να φτιάξουμε τον πίνακα αληθείας του τύπου. Είδαμε τους νόμους της προτασιακής λογικής, δηλαδή κάποιες βασικές λογικές ισοδυναμίες μεταξύ τύπων.
Είδαμε ότι για κάθε δυνατή στήλη ενός πίνακα αληθείας υπάρχει τύπος με αυτές τις αποτιμήσεις και κατασκευάσαμε ένα τέτοιο τύπο (που είναι σε Κανονική Διαξευκτική Μορφή).
Κάναμε μία εισαγωγή στην Κατηγορηματική Λογική. Είδαμε τους ποσοδείκτες
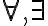 και είδαμε παραδείγματα τύπων.
και είδαμε παραδείγματα τύπων. Διαβάστε: σελ. 63-80 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Μιλήσαμε για τη θεμελίωση των φυσικών αριθμών. Ειδικότερα, είδαμε τα αξιώματα του Peano και τους αναδρομικούς ορισμούς των πράξεων της πρόσθεση και του πολλαπλασιασμού. Αποδείξαμε κάποιες βασικές ιδιότητες των πράξεων (αντιμεταθετικότητα, προσετεριστικότητα) χρησιμοποιώντας την Αρχή της Επαγωγής. Ορίσαμε την σχέση
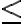 και είδαμε ότι είναι σχέση ολικής διάταξης στο
και είδαμε ότι είναι σχέση ολικής διάταξης στο 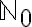 .
.Διαβάστε: σελ. 88-97 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Μιλήσαμε για την Αρχή της Επαγωγής και είδαμε κάποια παραδείγματα.
Είδαμε την Ισχυρή Επαγωγή και δείξαμε ότι ως αποδεικτική μέθοδος (αν και συχνά βολική) δεν είναι πραγματικά ισχυρότερη από την "απλή" επαγωγή. Ειδικότερα, δείξαμε ότι προκύπτει από την Αρχή της Επαγωγής.
Είδαμε την Αρχή του Ελαχίστου. Την αποδείξαμε με επαγωγή (ισχυρή). Είδαμε κάποια παραδείγματα.
Ορίσαμε το μέγιστο κοινό διαιρέτη δύο ακεραίων και δείξαμε ότι υπάρχει, αρκεί να μην είναι και οι δύο ίσοι με το 0. Δείξαμε ότι για
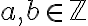 με
με 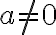 , το σύνολο
, το σύνολο έχει ελάχιστο στοιχείο, το οποίο είναι μεγιστος κοινός διαιρέτης των
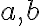 . Αν
. Αν 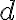 είναι ένας μ.κ.δ. των
είναι ένας μ.κ.δ. των 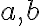 , τότε και το
, τότε και το 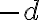 είναι επίσης ένας μ.κ.δ. Για να κάνουμε το μ.κ.δ. μοναδικό, παίρνουμε τον θετικό από τους δύο αριθμούς. Η απόδειξη αυτή μας δίνει επιπλέον, ότι ο
είναι επίσης ένας μ.κ.δ. Για να κάνουμε το μ.κ.δ. μοναδικό, παίρνουμε τον θετικό από τους δύο αριθμούς. Η απόδειξη αυτή μας δίνει επιπλέον, ότι οΜιλήσαμε για πρώτους αριθμούς και δείξαμε ότι είναι άπειροι. Δείξαμε ότι κάθε αριθμός γράφεται ως γινόμενο πρώτων.
Διαβάστε: σελ. 97-98 από τις σημειώσεις Χ. Κουρουνιώτη.
Διαβάστε: σελ. 98-101 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Δείξαμε ότι κάθε φυσικός αριθμός
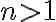 γράφεται ως γινόμενο πρώτων με μοναδικό κατ' ουσία τρόπο (εάν δηλαδή αλλάξουμε τη σειρά που γράφουμε τους πρώτους στο γινόμενο δεν θεωρείται διαφορετική γραφή).
γράφεται ως γινόμενο πρώτων με μοναδικό κατ' ουσία τρόπο (εάν δηλαδή αλλάξουμε τη σειρά που γράφουμε τους πρώτους στο γινόμενο δεν θεωρείται διαφορετική γραφή). Είδαμε ξανά το σύνολο
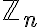 και τις πράξεις της πρόσθεσης και του πολλαπλασιασμού κλάσεων. Δείξαμε ότι οι πράξεις είναι αντιμεταθετικές, προσεταιριστικές, ισχύει η επιμεριστική ιδιότητα. Είδαμε ότι αν ο
και τις πράξεις της πρόσθεσης και του πολλαπλασιασμού κλάσεων. Δείξαμε ότι οι πράξεις είναι αντιμεταθετικές, προσεταιριστικές, ισχύει η επιμεριστική ιδιότητα. Είδαμε ότι αν ο 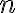 είναι πρώτος, τότε για κάθε κλάση
είναι πρώτος, τότε για κάθε κλάση 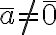 υπάρχει κλάση
υπάρχει κλάση 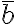 τέτοια ώστε
τέτοια ώστε 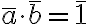 . Αυτό δεν ισχύει όταν έχουμε κλάσεις modulo κάποιο σύνθετο αριθμό
. Αυτό δεν ισχύει όταν έχουμε κλάσεις modulo κάποιο σύνθετο αριθμό 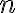 .
.Κάναμε μία εισαγωγή στη συνδυαστική. Ορίσαμε πότε ένα σύνολο είναι πεπερασμένο και ποιό είναι το πλήθος των στοιχείων του. Είδαμε την Αρχή του Αθροίσματος, την Αρχή του Γινομένου και την Αρχή Εγκλεισμού-Αποκλεισμού.
Διαβάστε: σελ. 101-102 από τις σημειώσεις Χ. Κουρουνιώτη.
Διαβάστε: σελ. 109-112 από τις σημειώσεις Χ. Κουρουνιώτη.
-
ΔΙΑΚΟΠΕΣ ΠΑΣΧΑ
-
ΔΙΑΚΟΠΕΣ ΠΑΣΧΑ
-
Ορίσαμε τους δυωνυμικούς συντελεστές
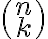 για
για 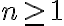 και
και 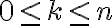 , δείξαμε ότι ικανοποιούν τις σχέσεις
, δείξαμε ότι ικανοποιούν τις σχέσειςΔείξαμε το δυωνυμικό θεώτημα:
Δείξαμε ότι το πλήθος των υποσυνόλων
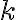 στοιχείων του συνόλου
στοιχείων του συνόλου 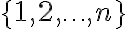 είναι επίσης ίσο με
είναι επίσης ίσο με 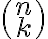 .
.Δείξαμε ότι το πλήθος των μεταθέσεων (διατάξεων)
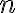 αντικειμένων είναι ίσο με
αντικειμένων είναι ίσο με 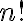
Είδαμε παραδείγματα.
Δείξαμε ότι το πλήθος ακέραιων λύσεων της εξίσωσης
Είδαμε τη γενίκευση του δυωνυμικού θεωρήματος:
Ο συντελεστής
εκφράζει το πλήθος των διατάξεων
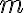 ομάδων όμοιων αντικειμένων, όπου η ομάδα
ομάδων όμοιων αντικειμένων, όπου η ομάδα  έχει
έχει 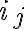 (όμοια μεταξύ τους) αντικείμενα. Ισοδύναμα, είναι το πλήθος των αναγραμματισμών μίας λέξης
(όμοια μεταξύ τους) αντικείμενα. Ισοδύναμα, είναι το πλήθος των αναγραμματισμών μίας λέξης 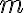 διακεκριμένων γραμμάτων, όπου το 1ο γράμμα εμφανίζεται
διακεκριμένων γραμμάτων, όπου το 1ο γράμμα εμφανίζεται 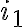 φορές, το 2ο γράμμα
φορές, το 2ο γράμμα 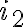 φορές κλπ και
φορές κλπ και 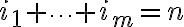 .
.Διαβάστε: σελ. 112-120 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Μιλήσαμε για πληθαρίθμους άπειρων συνόλων. Ορίσαμε δύο σύνολα
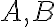 έχουν τον ίδιο πληθάριθμο, όταν υπάρχει αμφιμονοσήμαντη συνάρτηση
έχουν τον ίδιο πληθάριθμο, όταν υπάρχει αμφιμονοσήμαντη συνάρτηση 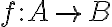 . Είδαμε παραδείγματα. Οναμάσαμε ένα σύνολο αριθμήσιμο, αν είναι πεπερασμένο ή αν έχει τον ίδιο πληθάριθμο με το
. Είδαμε παραδείγματα. Οναμάσαμε ένα σύνολο αριθμήσιμο, αν είναι πεπερασμένο ή αν έχει τον ίδιο πληθάριθμο με το 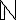 . Είδαμε παραδείγματα αριθμήσιμων συνόλων.
. Είδαμε παραδείγματα αριθμήσιμων συνόλων.Διαβάστε: σελ. 121-125 από τις σημειώσεις Χ. Κουρουνιώτη.
-
Δείξαμε ότι το δυναμοσύνολο
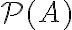 ενός συνόλου
ενός συνόλου  έχει αυστηρά μεγαλύτερο πληθάριθμο από το σύνολο
έχει αυστηρά μεγαλύτερο πληθάριθμο από το σύνολο  . Δηλαδή, υπάρχει απεικόνιση
. Δηλαδή, υπάρχει απεικόνιση 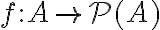 η οποία είναι 1-1, αλλά δεν υπάρχει απεικόνιση
η οποία είναι 1-1, αλλά δεν υπάρχει απεικόνιση 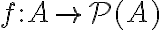 η οποία είναι επί. Στη συνέχεια είδαμε ότι ο πληθάριθμος του συνόλου
η οποία είναι επί. Στη συνέχεια είδαμε ότι ο πληθάριθμος του συνόλου 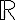 των πραγματικών αριθμών είναι ίσος με τον πληθάριθμο του δυναμοσυνόλου
των πραγματικών αριθμών είναι ίσος με τον πληθάριθμο του δυναμοσυνόλου 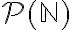 των φυσικών. Αυτό και η παραπάνω πρόταση μας δίνουν σαν συμπέρασμα ότι ο πληθάριθμος των πραγματικών αριθμών είναι αυστηρά μεγαλύτερος από τον πληθάριθμο των φυσικών: οι πραγματικοί αριθμοί δεν είναι αριθμήσιμο σύνολο. Η ίδια απόδειξη μπορεί να γίνει και με το διαγώνιο επιχείρημα του Cantor, που επίσης είδαμε.
των φυσικών. Αυτό και η παραπάνω πρόταση μας δίνουν σαν συμπέρασμα ότι ο πληθάριθμος των πραγματικών αριθμών είναι αυστηρά μεγαλύτερος από τον πληθάριθμο των φυσικών: οι πραγματικοί αριθμοί δεν είναι αριθμήσιμο σύνολο. Η ίδια απόδειξη μπορεί να γίνει και με το διαγώνιο επιχείρημα του Cantor, που επίσης είδαμε.Διαβάστε: σελ. 125-129 από τις σημειώσεις Χ. Κουρουνιώτη
-
Λύσαμε ασκήσεις.
-
Την Τετάρτη 28 Μαΐου, 11:00-14:00 θα γίνει ένα τελευταίο φροντιστήριο, στην αίθουσα Α212, για απορίες, από τον κύριο Σταυρακάκη. Σε αυτό το φροντιστήριο θα συζητήσετε (κάποιες) από τις επαναληπτικές ασκήσεις.


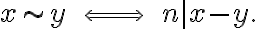
![[x] = \{y\in A : y\sim x\}. [x] = \{y\in A : y\sim x\}.](https://elearn.uoc.gr/filter/tex/pix.php/6b9d86e7ae331fa458eb518e7e43f9e9.gif)
![A /\sim\ \ =\ \{[x] : x\in A\}. A /\sim\ \ =\ \{[x] : x\in A\}.](https://elearn.uoc.gr/filter/tex/pix.php/e334a503f0d37abc087c187df6a3beb3.gif)
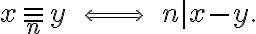
![\mathbb{Z} /\equiv_n\ \ =\ \{[0],[1],\ldots,[n-1]\} \mathbb{Z} /\equiv_n\ \ =\ \{[0],[1],\ldots,[n-1]\}](https://elearn.uoc.gr/filter/tex/pix.php/7c345f35655ebd7631bccbdf08dba9d8.gif)