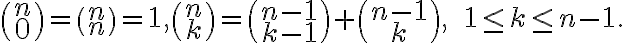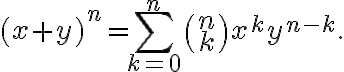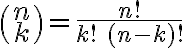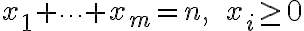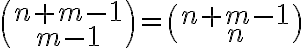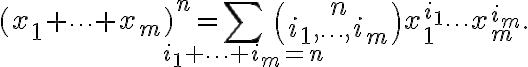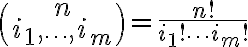27 Απριλίου - 3 Μαΐου
Section outline
-
Ορίσαμε τους δυωνυμικούς συντελεστές
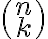 για
για 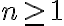 και
και 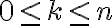 , δείξαμε ότι ικανοποιούν τις σχέσεις
, δείξαμε ότι ικανοποιούν τις σχέσειςΔείξαμε το δυωνυμικό θεώτημα:
Δείξαμε ότι το πλήθος των υποσυνόλων
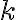 στοιχείων του συνόλου
στοιχείων του συνόλου 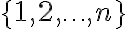 είναι επίσης ίσο με
είναι επίσης ίσο με 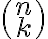 .
.Δείξαμε ότι το πλήθος των μεταθέσεων (διατάξεων)
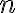 αντικειμένων είναι ίσο με
αντικειμένων είναι ίσο με 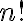
Είδαμε παραδείγματα.
Δείξαμε ότι το πλήθος ακέραιων λύσεων της εξίσωσης
Είδαμε τη γενίκευση του δυωνυμικού θεωρήματος:
Ο συντελεστής
εκφράζει το πλήθος των διατάξεων
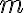 ομάδων όμοιων αντικειμένων, όπου η ομάδα
ομάδων όμοιων αντικειμένων, όπου η ομάδα  έχει
έχει 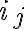 (όμοια μεταξύ τους) αντικείμενα. Ισοδύναμα, είναι το πλήθος των αναγραμματισμών μίας λέξης
(όμοια μεταξύ τους) αντικείμενα. Ισοδύναμα, είναι το πλήθος των αναγραμματισμών μίας λέξης 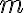 διακεκριμένων γραμμάτων, όπου το 1ο γράμμα εμφανίζεται
διακεκριμένων γραμμάτων, όπου το 1ο γράμμα εμφανίζεται 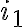 φορές, το 2ο γράμμα
φορές, το 2ο γράμμα 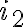 φορές κλπ και
φορές κλπ και 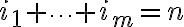 .
.Διαβάστε: σελ. 112-120 από τις σημειώσεις Χ. Κουρουνιώτη.