23 Φεβρουαρίου - 1 Μαρτίου
Section outline
-
Δεδομένης μίας σχέσης ισοδυναμίας
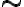 σε ένα σύνολο
σε ένα σύνολο 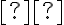 , ορίσαμε την κλάση του στοιχείου
, ορίσαμε την κλάση του στοιχείου  ως το σύνολο των στοιχείων του
ως το σύνολο των στοιχείων του  που είναι ισοδύναμα με το
που είναι ισοδύναμα με το 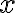
Συμβολίσαμε το σύνολο όλων των κλάσεων της σχέσης
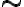 με
με Μελετήσαμε τη σχέση
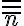 (ορισμένη στο
(ορισμένη στο 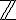 για ένα σταθεροποιημένο μη μηδενικό
για ένα σταθεροποιημένο μη μηδενικό 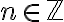 ),
),Δείξαμε ότι
και ότι όλες οι παραπάνω κλάσεις είναι ανά δύο διαφορετικές.
Είδαμε ότι οι κλάσεις ισοδυναμίας ορίζουν μία διαμέριση του συνόλου και αντίστροφα: κάθε διαμέριση του συνόλου
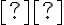 ορίζει μία σχέση ισοδυναμίας.
ορίζει μία σχέση ισοδυναμίας.Ορίσαμε την έννοια της σχέσης διάταξης και είδαμε παραδείγματα.
Σε ένα σύνολο
 , στο οποίο έχουμε ορίσει μία σχέση διάταξης, ορίσαμε την έννοια του μεγιστικού και την έννοια του μέγιστου στοιχείου. Είδαμε ότι μπορεί να υπάρχουν πολλά μεγιστικά στοιχεία. Όταν υπάρχει μέγιστο στοιχείο, αυτό είναι μοναδικό και είναι το μοναδικό μεγιστικό στοιχείο του
, στο οποίο έχουμε ορίσει μία σχέση διάταξης, ορίσαμε την έννοια του μεγιστικού και την έννοια του μέγιστου στοιχείου. Είδαμε ότι μπορεί να υπάρχουν πολλά μεγιστικά στοιχεία. Όταν υπάρχει μέγιστο στοιχείο, αυτό είναι μοναδικό και είναι το μοναδικό μεγιστικό στοιχείο του  (πάντα ως προς τη σχέση διάταξης την οποία μελατάμε).
(πάντα ως προς τη σχέση διάταξης την οποία μελατάμε).Ορίσαμε την έννοια της συνάρτησης
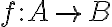 , με πεδίο ορισμού
, με πεδίο ορισμού  και πεδίο τιμών
και πεδίο τιμών 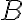 .
. Ορίσαμε πότε μία συνάρτηση είναι ένα-προς-ένα και πότε είναι επί.
Ορίσαμε τη σύθεση συναρτήσεων και την έννοια της αντίστροφης συνάρτησης, μίας δεδομένης συνάρτησης
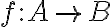 .
.Διαβάστε: σελ. 24-31 από τις σημειώσεις Χ. Κουρουνιώτη.
Διαβάστε: σελ. 32-49 από τις σημειώσεις Χ. Κουρουνιώτη.


![[x] = \{y\in A : y\sim x\}. [x] = \{y\in A : y\sim x\}.](https://elearn.uoc.gr/filter/tex/pix.php/6b9d86e7ae331fa458eb518e7e43f9e9.gif)
![A /\sim\ \ =\ \{[x] : x\in A\}. A /\sim\ \ =\ \{[x] : x\in A\}.](https://elearn.uoc.gr/filter/tex/pix.php/e334a503f0d37abc087c187df6a3beb3.gif)
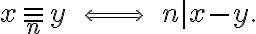
![\mathbb{Z} /\equiv_n\ \ =\ \{[0],[1],\ldots,[n-1]\} \mathbb{Z} /\equiv_n\ \ =\ \{[0],[1],\ldots,[n-1]\}](https://elearn.uoc.gr/filter/tex/pix.php/7c345f35655ebd7631bccbdf08dba9d8.gif)