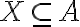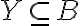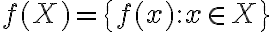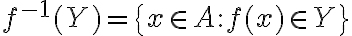2 Μαρτίου - 8 Μαρτίου
Section outline
-
Μελετήσαμε τις έννοιες του αριστερού/δεξιού αντιστρόφου μίας συνάρτησης
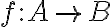 .
.Δείξαμε ότι
- η συνάρτηση
 έχει αριστερό αντίστροφο αν και μόνο αν είναι 1-1.
έχει αριστερό αντίστροφο αν και μόνο αν είναι 1-1. - η συνάρτηση
 έχει δεξιό αντίστροφο αν και μόνο αν είναι επί.
έχει δεξιό αντίστροφο αν και μόνο αν είναι επί.
Δείξαμε ότι η
 είναι αντιστρέψιμη αν και μόνο αν είναι 1-1 και επί. Σε αυτή την περίπτωση η αντίστροφη συνάρτηση είναι μοναδική και συμβολίζεται
είναι αντιστρέψιμη αν και μόνο αν είναι 1-1 και επί. Σε αυτή την περίπτωση η αντίστροφη συνάρτηση είναι μοναδική και συμβολίζεται 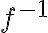 .
. Ονομάσαμε την εικόνα του συνόλου
 , εικόνα της συνάρτησης
, εικόνα της συνάρτησης  και τη συμβολίσαμε με
και τη συμβολίσαμε με 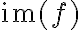 . Με άλλα λόγια,
. Με άλλα λόγια, 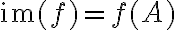 .
.Διαβάστε: σελ. 49-53 από τις σημειώσεις Χ. Κουρουνιώτη.
- η συνάρτηση