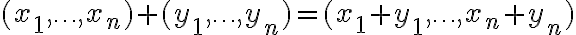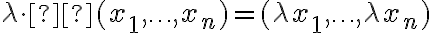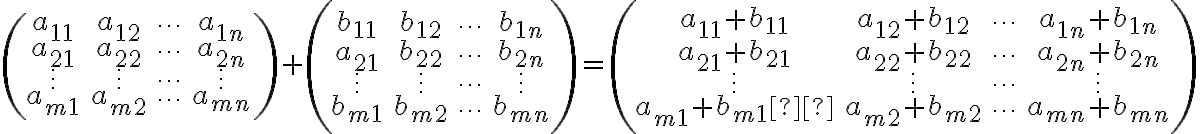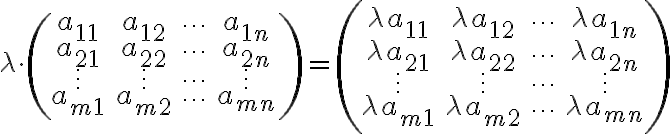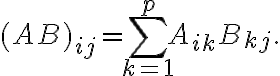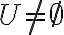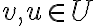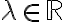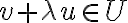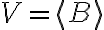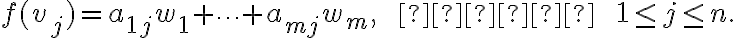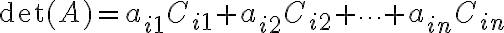ΒΙΟ101.1 - Εισαγωγή στα Μαθηματικά / Γραμμική Άλγεβρα
Section outline
-
ΒΙΟ101 - Εισαγωγή στα Μαθηματικά / Γραμμική Άλγεβρα ΠΜΣ Βιοπληροφορική Μονοτμηματικό Έδρα Τμήμα Iατρικής Σχολή Επιστημών Υγείας Πανεπιστημίου Κρήτης ΦΕΚ 598/7.3.2016 τ.Β’ Διευθυντής Σπουδών Νεκτάριος Ταβερναράκης
Καθηγητής Μοριακής Βιολογίας - Βιολογίας ΣυστημάτωνΑναπληρωτής
Διευθυντής ΣπουδώνΙωάννης Ηλιόπουλος
Επικουρος Καθηγητής
Μοριακής Βιολογίας - Γονιδιωματικής ΒιοπληροφορικήςΥπεύθυνος Μαθήματος: Διδάσκοντες Μαθήματος: Θεόδουλος Γαρεφαλάκης, Μαρία Λουκάκη Γραμματεία ΠΜΣ 2810.39.4615
2810.39.4868
2810.39.4526FAX 2810.39.4569 E-Mail postgradsecr@med.uoc.gr website http://msc_bioinformatics.med.uoc.gr/ Γενικές Πληροφορίες
Διδάσκοντες Θεόδουλος Γαρεφαλάκης (γραφείο Γ216, email: tgaref@uoc.gr)
Μαρία Λουκάκη (γραφείο Γ315, email: mloukaki@uoc.gr)
Ώρες Μαθήματος Δευτέρα 9:00 - 11:00 (αίθουσα Β212, κτήριο ΤΜΕΜ)
Τετάρτη 9:00 - 11:00 (αίθουσα Β212, κτήριο ΤΜΕΜ)
Περιγραφή Μαθήματος
Στο μάθημα θα δούμε βασικές έννοιες της Γραμμικής Άλγεβρας. Θα επικεντρωθούμε στους χώρους
 και
και 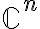 . Μπορείτε να βρείτε την ύλη του μαθήματος εδώ.
. Μπορείτε να βρείτε την ύλη του μαθήματος εδώ.Αξιολόγηση
Βιβλιογραφία
- Mια εισαγωγή στην Γραμμική Άλγεβρα, A. Morris
- Μια εισαγωγή στην Γραμμική Άλγεβρα για τις θετικές επιστήμες, Χαραλάμπους, Φωτιάδης
- Σημειώσεις Χ. Κουρουνιώτη
- Γραμμική Άλγεβρα και Εφαρμογές, G. Strang
- Μία εισαγωγή στην Γραμμική Άλγεβρα, Βάρσος, Δεριζιώτης, Εμμανουήλ, Μαλιάκας, Μελάς, Ταλλέλη
- Γραμμική Άλγεβρα, Θεοχάρη-Αποστολίδη, Βαβατσούλας, Χαραλάμπους
-
Ορίσαμε το σύνολο
 των
των 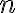 -άδων πραγματικών αριθμών και ορίσαμε δύο πράξεις:
-άδων πραγματικών αριθμών και ορίσαμε δύο πράξεις:Είδαμε τις βασικές ιδιότητες που ικανοποιούν οι πράξεις αυτές.
Είδαμε το σύνολο των
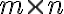 (
(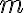 επί
επί 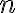 ) πινάκων
) πινάκων 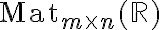 . Ένας
. Ένας 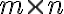 πίνακας είναι μία διάταξη αριθμών σε
πίνακας είναι μία διάταξη αριθμών σε 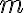 γραμμές και
γραμμές και 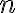 στήλες.
στήλες.
Συνήθως θα περιγράφουμε ένα τέτοιο πίνακα δίνοντας τα στοιχεία του
δίνοντας τα στοιχεία του 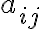 για
για 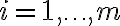 ,
, 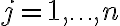 .
.
Oρίσαμε δύο πράξεις αντίστοιχες με αυτές του :
:Είδαμε ότι οι πράξεις της πρόσθεσης πινάκων και του πολλαπλασιασμού αριθμού με πίνακα ικανοποιούν τις ίδιες ιδιότητες με τις αντίστοιχες πράξεις του
 .
.Ορίσαμε τον πολλαπλασιασμό πινάκων. Ειδικότερα, όταν
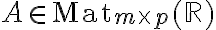 και
και 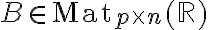 , (δηλαδή το πλήθος στηλών του
, (δηλαδή το πλήθος στηλών του  είναι ίσο με το πλήθος γραμμών του
είναι ίσο με το πλήθος γραμμών του 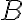 ) τότε ορίζεται το γινόμενο
) τότε ορίζεται το γινόμενο 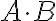 , το οποίο είναι ένας
, το οποίο είναι ένας 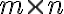 πίνακας. To
πίνακας. To 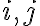 στοιχείο του πίνακα
στοιχείο του πίνακα 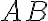 είναι το
είναι τοΟρίσαμε τις έννοιες του άνω (κάτω) τριγωνικού πίνακα, του διαγώνιου πίνακα, του συμμετρικού πίνακα.
Είδαμε βασικές ιδιότητες του πολλαπλασιασμού πινάκων. Ορίσαμε πότε ένας τετραγωνικός πίνακας είναι αντιστρέψιμος.
Αρχίσαμε να μελετάμε την έννοια της αντιστρεψιμότητας πινάκων. Είπαμε, χωρίς να το δικαιολογήσουμε, ότι για να είναι ένας πίνακας
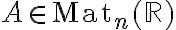 αντιστρέψιμος αρκεί να υπάρχει πίνακας
αντιστρέψιμος αρκεί να υπάρχει πίνακας 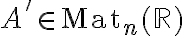 τέτοιος ώστε
τέτοιος ώστε 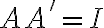 . Αν συμβαίνει αυτό, τότε είναι βέβαιο ότι θα ισχύει και
. Αν συμβαίνει αυτό, τότε είναι βέβαιο ότι θα ισχύει και 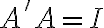 και άρα ο
και άρα ο  είναι αντιστρέψιμος. Δείξαμε ότι αν δύο πίνακες
είναι αντιστρέψιμος. Δείξαμε ότι αν δύο πίνακες 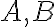 είναι αντιστρέψιμοι τότε το γινόμενο
είναι αντιστρέψιμοι τότε το γινόμενο 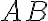 είναι αντιστρέψιμος πίνακας. Σε αυτή την περίπτωση ισχύει
είναι αντιστρέψιμος πίνακας. Σε αυτή την περίπτωση ισχύει 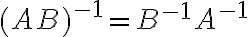 . Γενικότερα, αν οι πίνακες
. Γενικότερα, αν οι πίνακες 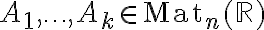 είναι αντιστρέψιμοι, τότε και ο πίνακας
είναι αντιστρέψιμοι, τότε και ο πίνακας  είναι αντιστρέψιμος και ισχύει
είναι αντιστρέψιμος και ισχύει 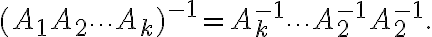
Αρχίσαμε να μιλάμε για απαλοιφή Gauss για τη λύση γραμμικών συστημάτων.
Διαβάστε: παρ. 2.1 από το βιβλίο [2].
-
Μιλήσαμε για επίλυση γραμμικών συστημάτων και περιγράψαμε τη μέθοδο της απαλοιφής Gauss. Ορίσαμε την τάξη ενός πίνακα ως το πλήθος των οδηγών στον κλιμακωτό πίνακα που καταλήγει η απαλοιφή Gauss. Ορίσαμε τις βασικές και τις ελεύθερες μεταβλητές και είδαμε πώς να περιγράφουμε τη γενική λύση του συστήματος συναρτήσει των ελεύθερων μεταβλητών.
Είδαμε ότι ένας
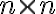 πίνακας
πίνακας  είναι αντιστρέψιμος αν και μόνο αν μετά την απαλοιφή Gauss προκύπτουν
είναι αντιστρέψιμος αν και μόνο αν μετά την απαλοιφή Gauss προκύπτουν 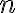 οδηγοί, δηλαδή ο πίνακας έχει τάξη ίση με
οδηγοί, δηλαδή ο πίνακας έχει τάξη ίση με 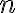 .
.Είδαμε τη μέθοδο Gauss-Jordan για τον υπολογισμό του αντίστροφου πίνακα, εφόσον υπάρχει.
Είδαμε την ανάλυση
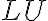 του πίνακα
του πίνακα  .
. Διαβάστε: παρ. 1.1, 1.2 από το βιβλίο [2].
Διαβάστε: παρ. 2.2 από το βιβλίο [2].
-
Είδαμε την έννοια του υπόχωρου ενός διανυσματικού χώρου. Ειδικότερα, δείξαμε ότι αν
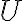 είναι ένα υποσύνολο του
είναι ένα υποσύνολο του  , τότε είναι υπόχωρος του
, τότε είναι υπόχωρος του  αν
αν Είδαμε παραδείματα.
Αν
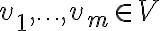 τότε ορίσαμε τον υπόχωρο που παράγεται από τα
τότε ορίσαμε τον υπόχωρο που παράγεται από τα 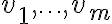 ως το σύνολο
ως το σύνολο 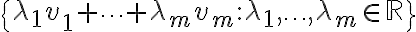 και το συμβολίσαμε με
και το συμβολίσαμε με 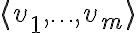 .
.Είδαμε επίσης, ότι αν
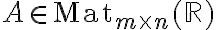 τότε το σύνολο λύσεων του ομογενούς συστήματος
τότε το σύνολο λύσεων του ομογενούς συστήματος 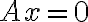 είναι υπόχωρος του
είναι υπόχωρος του  .
.Ορίσαμε πότε ένα σύνολο διανυσμάτων
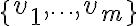 είναι γραμμικώς εξαρτημένο/ανεξάρτητο και είδαμε παραδείγματα. Είδαμε πώς μπορούμε να εξετάζουμε (αλγοριθμικά) εάν ένα δεδομένο σύνολο είναι εξαρτημένο/ανεξάρτητο. Εάν
είναι γραμμικώς εξαρτημένο/ανεξάρτητο και είδαμε παραδείγματα. Είδαμε πώς μπορούμε να εξετάζουμε (αλγοριθμικά) εάν ένα δεδομένο σύνολο είναι εξαρτημένο/ανεξάρτητο. Εάν  είναι ένας υπόχωρος του
είναι ένας υπόχωρος του  και
και 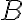 ένα σύνολο διανυσμάτων του, λέμε ότι το
ένα σύνολο διανυσμάτων του, λέμε ότι το 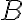 είναι βάση του
είναι βάση του  εάν:
εάν:Είδαμε ότι η απαίτηση της γραμμικής ανεξαρτησίας του
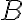 εξασφαλίζει ότι κανένα γνήσιο υποσύνολο του
εξασφαλίζει ότι κανένα γνήσιο υποσύνολο του 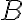 δεν παράγει τον
δεν παράγει τον  . Με άλλα λόγια κάθε διάνυσμα του
. Με άλλα λόγια κάθε διάνυσμα του 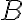 είναι απαραίτητο.
είναι απαραίτητο. Διαβάστε: παρ. 3.2 από το βιβλίο [2].
Διαβάστε: παρ. 3.3 έως τη σελ. 89 από το βιβλίο [2].
-
Είδαμε παραδείγματα βάσεων διανυσματικών χώρων. Για ένα δεδομένο πίνακα
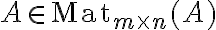 , είδαμε πώς μπορούμε να υπολογίζουμε μία βάση του μηδενόχωρου του,
, είδαμε πώς μπορούμε να υπολογίζουμε μία βάση του μηδενόχωρου του, 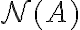 και μία βάση του χώρου στηλών του,
και μία βάση του χώρου στηλών του, 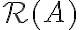 .
.Είδαμε ότι αν
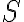 είναι ένα γραμμικώς ανεξάρτητο σύνολο διανυσμάτων ενός χώρου
είναι ένα γραμμικώς ανεξάρτητο σύνολο διανυσμάτων ενός χώρου  , και
, και 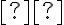 ένα σύνολο διανυσμάτων που παράγει τον
ένα σύνολο διανυσμάτων που παράγει τον  (δηλαδή
(δηλαδή 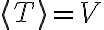 ), τότε
), τότε 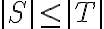 και ότι το σύνολο
και ότι το σύνολο 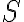 μπορεί να συμπληρωθεί σε βάση του
μπορεί να συμπληρωθεί σε βάση του  . Χρησιμοποιώντας αυτό, δείξαμε ότι δύο οποιεσδήποτε βάσεις του
. Χρησιμοποιώντας αυτό, δείξαμε ότι δύο οποιεσδήποτε βάσεις του  περιέχουν το ίδιο πλήθος διανυσμάτων. Αυτό το πλήθος ονομάζεται διάσταση του χώρου. Για παράδειγμα, η διάσταστη του
περιέχουν το ίδιο πλήθος διανυσμάτων. Αυτό το πλήθος ονομάζεται διάσταση του χώρου. Για παράδειγμα, η διάσταστη του 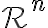 είναι ίση με
είναι ίση με 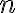 , αφού η κανονική του βάση,
, αφού η κανονική του βάση, 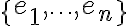 , περιέχει
, περιέχει 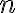 διανύσματα.
διανύσματα.Αν
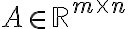 και
και 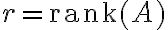 είναι η τάξη του πίνακα
είναι η τάξη του πίνακα 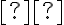 (δηλαδή το πλήθος των οδηγών στον κλιμακωτό πίνακα που προκύπτει από την απαλοιφή Gauss), τότε
(δηλαδή το πλήθος των οδηγών στον κλιμακωτό πίνακα που προκύπτει από την απαλοιφή Gauss), τότε 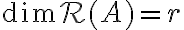 και
και 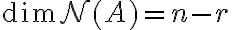 . Βλέπουμε ότι πάντα ισχύει
. Βλέπουμε ότι πάντα ισχύει 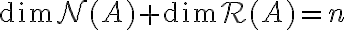 . Είπαμε επίσης, ότι
. Είπαμε επίσης, ότι 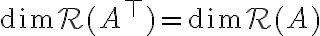 , δηλαδή η διάσταση του χώρου στηλών και η διάσταση του χώρου γραμμών ενός πίνακα είναι ίσες.
, δηλαδή η διάσταση του χώρου στηλών και η διάσταση του χώρου γραμμών ενός πίνακα είναι ίσες.Ορίσαμε την έννοια της γραμμικής απεικόνισης και είδαμε παραδείγματα.
Διαβάστε: παρ. 3.3 από το βιβλίο [2].
Διαβάστε: παρ. 3.4, 4.1 έως τη σελ. 108 από το βιβλίο [2].
-
Είδαμε ότι για κάθε γραμμική απεικόνιση
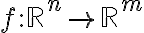 , υπάρχει ένας (μοναδικός) πίνακας
, υπάρχει ένας (μοναδικός) πίνακας 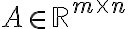 , τέτοιος ώστε
, τέτοιος ώστε 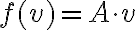 για κάθε
για κάθε 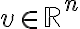 . Αυτός ο πίνακας ονομάζεται πίνακας της
. Αυτός ο πίνακας ονομάζεται πίνακας της  και τον συμβολίζουμε με
και τον συμβολίζουμε με ![[f] [f]](https://elearn.uoc.gr/filter/tex/pix.php/7b93cec8a8b3e110392556212941efcd.gif) .
. Είδαμε ότι μπορούμε να γενικεύσουμε τον παραπάνω ορισμό ως εξής: αν θεωρήσουμε μία βάση
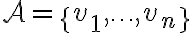 του
του  και μία βάση
και μία βάση 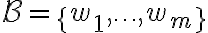 του
του 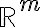 , τότε
, τότε Ο πίνακας
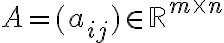 ονομάζεται πίνακας της
ονομάζεται πίνακας της  ως προς τις βάσεις
ως προς τις βάσεις 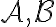 και τον συμβολίζουμε με
και τον συμβολίζουμε με ![[f]_{\mathcal{A}}^{\mathcal{B}} [f]_{\mathcal{A}}^{\mathcal{B}}](https://elearn.uoc.gr/filter/tex/pix.php/b06f260e0079d40e1b534a73ca3e3054.gif) . Ο πίνακας της
. Ο πίνακας της  είναι ο πίνακας ως προς τις κανονικές βάσεις,
είναι ο πίνακας ως προς τις κανονικές βάσεις, 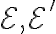 , των
, των  και
και 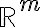 αντίστοιχα.
αντίστοιχα.Διαβάστε: παρ. 4.1 από το βιβλίο [2].
-
Είδαμε τη σύνθεση γραμμικών απεικονίσεων, η οποία είναι επίσης γραμμική απεικόνιση. Ειδικότερα, θεωρούμε τους χώρους
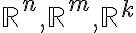 και τις βάσεις
και τις βάσεις 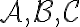 αντίστοιχα. Είδαμε ότι αν
αντίστοιχα. Είδαμε ότι αν 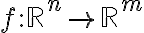 και
και 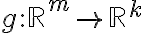 είναι γραμμικές απεικονίσεις, τότε η σύνθεση τους
είναι γραμμικές απεικονίσεις, τότε η σύνθεση τους 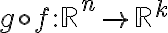 με τύπο
με τύπο 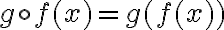 είναι γραμμική και
είναι γραμμική και ![[g\circ f]_{\mathcal{A}}^{\mathcal{C}} = [g]_{\mathcal{B}}^{\mathcal{C}} \cdot [f]_{\mathcal{A}}^{\mathcal{B}}. [g\circ f]_{\mathcal{A}}^{\mathcal{C}} = [g]_{\mathcal{B}}^{\mathcal{C}} \cdot [f]_{\mathcal{A}}^{\mathcal{B}}.](https://elearn.uoc.gr/filter/tex/pix.php/aa95929de9301ff37cf5fa6d7f7a2fb6.gif)
Αν
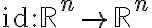 είναι η ταυτοτική απεικόνιση,
είναι η ταυτοτική απεικόνιση, 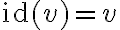 και
και 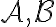 είναι δύο βάσεις του
είναι δύο βάσεις του  , τότε ο πίνακας
, τότε ο πίνακας ![[\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}} [\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}}](https://elearn.uoc.gr/filter/tex/pix.php/cfe72e53b9bcb2181fb00be7f756a61f.gif) είναι ο πίνακας αλλαγής βάσης από τη βάση
είναι ο πίνακας αλλαγής βάσης από τη βάση 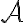 στην βάση
στην βάση 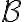 .
. Ορίσαμε τον πυρήνα και την εικόνα μίας γραμμικής απεικόνισης. Αν
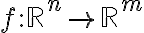 και
και 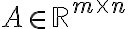 είναι ο πίνακας της
είναι ο πίνακας της  , δείξαμε ότι
, δείξαμε ότι 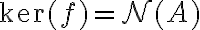 και
και 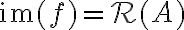 . Είδαμε παραδείγματα.
. Είδαμε παραδείγματα.Ορίσαμε τις έννοιες του μονομορφισμού, του επιμορφισμού και του ισομορφισμού.
Διαβάστε: παρ. 4.3 από το βιβλίο [2].
Διαβάστε: παρ. 4.2 από το βιβλίο [2].
-
Ορίσαμε την έννοια της ορίζουσας ενός
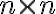 πίνακα
πίνακα 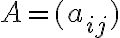 . Είδαμε ότι η ορίζουσα μπορεί να αναπτυχθεί ως προς οποιαδήποτε γραμμή και ισούται με
. Είδαμε ότι η ορίζουσα μπορεί να αναπτυχθεί ως προς οποιαδήποτε γραμμή και ισούται με όπου η παραπάνω σχέση είναι το ανάπτυγμα ως προς την γραμμή
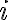 και
και 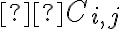 είναι ο i,j-συμπαράγοντας του Α. Δηλαδή
είναι ο i,j-συμπαράγοντας του Α. Δηλαδή 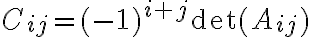 όπου
όπου 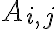 είναι ο
είναι ο 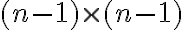 πίνακας που προκύπτει από τον A αν διαγράψουμε την i-γραμμή και τη j-στήλη. Είδαμε βασικές ιδιότητες της ορίζουσας:
πίνακας που προκύπτει από τον A αν διαγράψουμε την i-γραμμή και τη j-στήλη. Είδαμε βασικές ιδιότητες της ορίζουσας: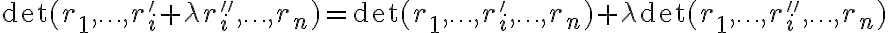
- Αν δύο γραμμές του Α είναι ίδιες τότε
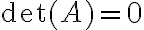
-
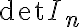 =1
=1 - Αν εναλλάξουμε δύο γραμμές του πίνακα η ορίζουσα αλλάζει πρόσημο
- Αν ο πίνακας B προκύπτει από τον πίνακα A προσθέτοντας στην γραμμή i ένα πολλαπλάσιο της γραμμής j, τότε η ορίζουσα παραμένει ίδια, δηλαδή
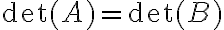
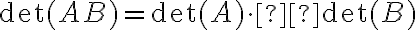
- Αν ο πίνακας A είναι άνω (ή κάτω) τριγωνικός, τότε η ορίζουσα του είναι ίση με το γινόμενο των στοιχείων της διαγωνίου.
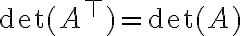 (και άρα μπορούμε να πάρουμε ανάπτυγμα ορίζουσας ως προς οποιαδήποτε στήλη και όχι μόνο γραμμή)
(και άρα μπορούμε να πάρουμε ανάπτυγμα ορίζουσας ως προς οποιαδήποτε στήλη και όχι μόνο γραμμή)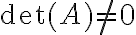 αν και μόνο αν Α είναι αντιστρέψιμος.
αν και μόνο αν Α είναι αντιστρέψιμος.
Κάναμε παραδείγματα υπολογισμού οριζουσών και είδαμε σαν εφαρμογή ότι μπορούμε να υπολογίσουμε τον αντίστροφο (αν υπάρχει) ενός πίνακα Α σαν
όπου
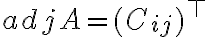 είναι ο ανάστροφος του πίνακα συμπαραγόντων του Α.
είναι ο ανάστροφος του πίνακα συμπαραγόντων του Α.Διαβάστε: παρ.2.3 από το [2]
-
Την Δευτέρα δεν έγινε μάθημα (17/11) και την Τετάρτη μιλήσαμε για δύο ακόμη εφαρμογές των οριζουσών την Μέθοδο Cramer και τον υπολογισμό όγκου $n$-διάστατου παραλ/δου.
Επίσης ορίσαμε την έννοια ιδιοτιμής-ιδιοδιανύσματος για πίνακες
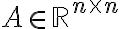 (και ισοδύναμα γραμμικές απεικονίσεις) σαν τον πραγματικό λ ώστε
(και ισοδύναμα γραμμικές απεικονίσεις) σαν τον πραγματικό λ ώστε 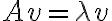 για κάποιο μη μηδενικό διάνυσμα v. Το v ονομάζουμε ιδιοδιάνυσμα του Α ως προς την ιδιοτιμή λ.
για κάποιο μη μηδενικό διάνυσμα v. Το v ονομάζουμε ιδιοδιάνυσμα του Α ως προς την ιδιοτιμή λ.Δείξαμε ότι το σύνολο των ιδιοδιανυσμάτων που αντιστοιχούν στην ιδιοτιμή λ είναι υπόχωρος του
 και ονομάζεται ιδιόχωρος του πίνακα. Επίσης ορίσαμε το χαρακτηριστικό πολυώνυμο ενός πίνακα. Τέλος είδαμε μεθοδολογία υπολογισμού ιδιοτιμών-ιδιοχώρων ενός πίνακα.
και ονομάζεται ιδιόχωρος του πίνακα. Επίσης ορίσαμε το χαρακτηριστικό πολυώνυμο ενός πίνακα. Τέλος είδαμε μεθοδολογία υπολογισμού ιδιοτιμών-ιδιοχώρων ενός πίνακα. Διαβάστε παρ. 5.1 από το [2]
-
Αυτή την εβδομάδα συνεχίσαμε να μιλάμε για ιδιοτιμές και ιδιοδιανύσματα ενός πίνακα και είδαμε πότε ένας πίνακας είναι διαγωνίσιμος. Μιλήσαμε για αλγεβρική και γεωμετρική πολλαπλότητα ιδιοτιμών και είδαμε ότι για κάθε πίνακα Α και για κάθε ιδιοτιμή του λ η αλγεβρική πολλαπλότητα της λ είναι μεγαλύτερη ή ίση της γεωμετρικής πολλαπλότητας της λ.
Είδαμε ότι ένας πίνακας
, τότε ο πίνακας Α διαγωνιοποιείται αν και μόνο αν η αλγεβρική πολ/τα της κάθε ιδιοτιμής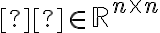 διαγωνιοποιείται αν και μόνο αν o
διαγωνιοποιείται αν και μόνο αν o 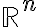 έχει βάση ιδιοδιανυσμάτων του. Αν μάλιστα το χαρακτηριστικό πολυώνυμο του Α παραγοντοποιείται σαν γινόμενο πρωτοβάθμιων (με κάποιους εκθέτες) δηλ.
έχει βάση ιδιοδιανυσμάτων του. Αν μάλιστα το χαρακτηριστικό πολυώνυμο του Α παραγοντοποιείται σαν γινόμενο πρωτοβάθμιων (με κάποιους εκθέτες) δηλ. 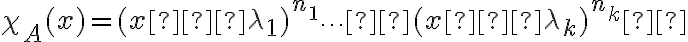
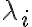 ισούται με την αντίστοιχη γεωμετρική της πολ/τα.
ισούται με την αντίστοιχη γεωμετρική της πολ/τα.
Τέλος είδαμε αρκετά παραδείγματα.
Διαβάστε παρ. 5.1-5.3 από το [2] (δεν εχουμε προλάβει να τελειώσουμε όλο το 5.3).
-
Την Δευτέρα είδαμε το Θεώρημα Cayley -Hamilton σύμφωνα με το οποίο κάθε πίνακας ικανοποιεί το χαρακτηριστικό πολυώνυμό του. Επίσης μιλήσαμε για το ελάχιστο πολυώνυμο ενός πίνακα, που είναι πάντα ένας διαιρέτης του χαρακτηριστικού. Τέλος δείξαμε ότι ένας πίνακας με k διαφορετικές ιδιοτιμές
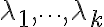 διαγωνιοποιείται αν και μόνο αν το ελάχιστο πολυώνυμό του είναι
διαγωνιοποιείται αν και μόνο αν το ελάχιστο πολυώνυμό του είναι  . Δώσαμε παραδείγματα.
. Δώσαμε παραδείγματα.Την Τετάρτη, μιλήσαμε για χώρους με εσωτερικό γινόμενο και είδαμε βασικές ιδιότητές του. Επίσης δείξαμε πως υπολογίζουμε το ορθογώνιο συμπλήρωμα ενός υποχώρου V του
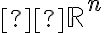 ως προς το συνηθισμένο εσωτερικό γινόμενο (dot product).
ως προς το συνηθισμένο εσωτερικό γινόμενο (dot product). Διαβάστε το υπόλοιπο από την 5.3 και συνεχίστε με την 5.4 (την οποία δεν τελειώσαμε).
-
Μιλήσαμε για ορθογώνια συμπληρώματα υποχώρων καθώς και για την προβολή διανύσματος σε υπόχωρο. Επίσης είδαμε την μέθοδο ορθοκανονικοποίησης Gram-Schmidt και την μέθοδο ελαχίστων τετραγώνων. Δόθηκαν πολλά παραδείγματα.
-
Λύσαμε ασκήσεις και παλιά θέματα εξετάσεων.