20 Οκτωβρίου - 26 Οκτωβρίου
Section outline
-
Είδαμε παραδείγματα βάσεων διανυσματικών χώρων. Για ένα δεδομένο πίνακα
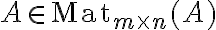 , είδαμε πώς μπορούμε να υπολογίζουμε μία βάση του μηδενόχωρου του,
, είδαμε πώς μπορούμε να υπολογίζουμε μία βάση του μηδενόχωρου του, 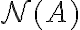 και μία βάση του χώρου στηλών του,
και μία βάση του χώρου στηλών του, 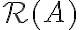 .
.Είδαμε ότι αν
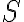 είναι ένα γραμμικώς ανεξάρτητο σύνολο διανυσμάτων ενός χώρου
είναι ένα γραμμικώς ανεξάρτητο σύνολο διανυσμάτων ενός χώρου  , και
, και 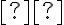 ένα σύνολο διανυσμάτων που παράγει τον
ένα σύνολο διανυσμάτων που παράγει τον  (δηλαδή
(δηλαδή 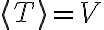 ), τότε
), τότε 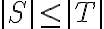 και ότι το σύνολο
και ότι το σύνολο 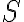 μπορεί να συμπληρωθεί σε βάση του
μπορεί να συμπληρωθεί σε βάση του  . Χρησιμοποιώντας αυτό, δείξαμε ότι δύο οποιεσδήποτε βάσεις του
. Χρησιμοποιώντας αυτό, δείξαμε ότι δύο οποιεσδήποτε βάσεις του  περιέχουν το ίδιο πλήθος διανυσμάτων. Αυτό το πλήθος ονομάζεται διάσταση του χώρου. Για παράδειγμα, η διάσταστη του
περιέχουν το ίδιο πλήθος διανυσμάτων. Αυτό το πλήθος ονομάζεται διάσταση του χώρου. Για παράδειγμα, η διάσταστη του 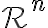 είναι ίση με
είναι ίση με 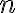 , αφού η κανονική του βάση,
, αφού η κανονική του βάση, 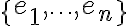 , περιέχει
, περιέχει 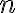 διανύσματα.
διανύσματα.Αν
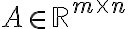 και
και 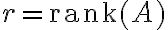 είναι η τάξη του πίνακα
είναι η τάξη του πίνακα 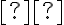 (δηλαδή το πλήθος των οδηγών στον κλιμακωτό πίνακα που προκύπτει από την απαλοιφή Gauss), τότε
(δηλαδή το πλήθος των οδηγών στον κλιμακωτό πίνακα που προκύπτει από την απαλοιφή Gauss), τότε 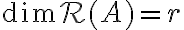 και
και 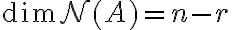 . Βλέπουμε ότι πάντα ισχύει
. Βλέπουμε ότι πάντα ισχύει 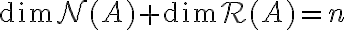 . Είπαμε επίσης, ότι
. Είπαμε επίσης, ότι 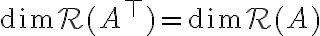 , δηλαδή η διάσταση του χώρου στηλών και η διάσταση του χώρου γραμμών ενός πίνακα είναι ίσες.
, δηλαδή η διάσταση του χώρου στηλών και η διάσταση του χώρου γραμμών ενός πίνακα είναι ίσες.Ορίσαμε την έννοια της γραμμικής απεικόνισης και είδαμε παραδείγματα.
Διαβάστε: παρ. 3.3 από το βιβλίο [2].
Διαβάστε: παρ. 3.4, 4.1 έως τη σελ. 108 από το βιβλίο [2].

