Section outline

  • Την Δευτέρα  είδαμε το Θεώρημα Cayley -Hamilton σύμφωνα με το οποίο κάθε πίνακας ικανοποιεί το χαρακτηριστικό πολυώνυμό του. Επίσης   μιλήσαμε για το ελάχιστο πολυώνυμο ενός πίνακα,  που είναι πάντα ένας διαιρέτης του χαρακτηριστικού. Τέλος δείξαμε ότι ένας πίνακας με  k διαφορετικές ιδιοτιμές 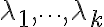\lambda _1, \cdots , \lambda_k   διαγωνιοποιείται αν και μόνο αν το ελάχιστο πολυώνυμό του είναι (x-\lambda_1)  \cdots  (x-\lambda_k) . Δώσαμε παραδείγματα.

    Την Τετάρτη, μιλήσαμε για χώρους με εσωτερικό γινόμενο και είδαμε βασικές ιδιότητές του. Επίσης δείξαμε πως υπολογίζουμε το ορθογώνιο συμπλήρωμα ενός υποχώρου V του 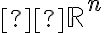  \mathbb{R}^n ως προς το συνηθισμένο εσωτερικό γινόμενο (dot product).   

    Διαβάστε το υπόλοιπο από την 5.3 και συνεχίστε με την 5.4 (την οποία δεν τελειώσαμε).