3 Νοεμβρίου - 9 Νοεμβρίου
Section outline
-
Είδαμε τη σύνθεση γραμμικών απεικονίσεων, η οποία είναι επίσης γραμμική απεικόνιση. Ειδικότερα, θεωρούμε τους χώρους
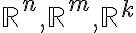 και τις βάσεις
και τις βάσεις 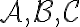 αντίστοιχα. Είδαμε ότι αν
αντίστοιχα. Είδαμε ότι αν 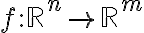 και
και 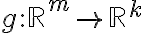 είναι γραμμικές απεικονίσεις, τότε η σύνθεση τους
είναι γραμμικές απεικονίσεις, τότε η σύνθεση τους 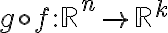 με τύπο
με τύπο 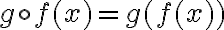 είναι γραμμική και
είναι γραμμική και ![[g\circ f]_{\mathcal{A}}^{\mathcal{C}} = [g]_{\mathcal{B}}^{\mathcal{C}} \cdot [f]_{\mathcal{A}}^{\mathcal{B}}. [g\circ f]_{\mathcal{A}}^{\mathcal{C}} = [g]_{\mathcal{B}}^{\mathcal{C}} \cdot [f]_{\mathcal{A}}^{\mathcal{B}}.](https://elearn.uoc.gr/filter/tex/pix.php/aa95929de9301ff37cf5fa6d7f7a2fb6.gif)
Αν
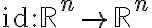 είναι η ταυτοτική απεικόνιση,
είναι η ταυτοτική απεικόνιση, 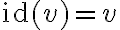 και
και 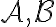 είναι δύο βάσεις του
είναι δύο βάσεις του  , τότε ο πίνακας
, τότε ο πίνακας ![[\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}} [\mathrm{id}]_{\mathcal{A}}^{\mathcal{B}}](https://elearn.uoc.gr/filter/tex/pix.php/cfe72e53b9bcb2181fb00be7f756a61f.gif) είναι ο πίνακας αλλαγής βάσης από τη βάση
είναι ο πίνακας αλλαγής βάσης από τη βάση 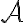 στην βάση
στην βάση 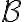 .
. Ορίσαμε τον πυρήνα και την εικόνα μίας γραμμικής απεικόνισης. Αν
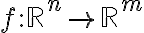 και
και 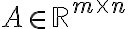 είναι ο πίνακας της
είναι ο πίνακας της  , δείξαμε ότι
, δείξαμε ότι 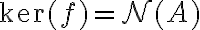 και
και 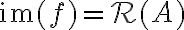 . Είδαμε παραδείγματα.
. Είδαμε παραδείγματα.Ορίσαμε τις έννοιες του μονομορφισμού, του επιμορφισμού και του ισομορφισμού.
Διαβάστε: παρ. 4.3 από το βιβλίο [2].
Διαβάστε: παρ. 4.2 από το βιβλίο [2].

