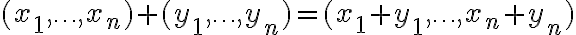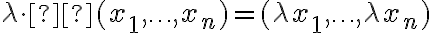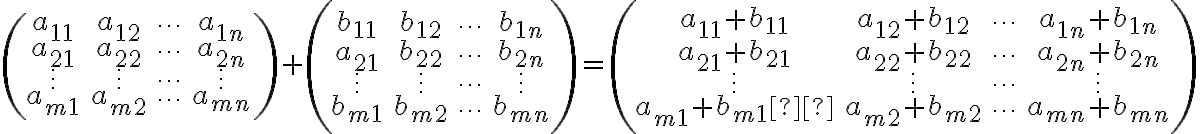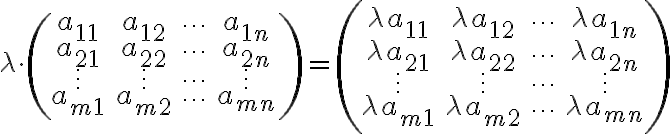29 Σεπτεμβρίου - 5 Οκτωβρίου
Section outline
-
Ορίσαμε το σύνολο
 των
των 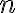 -άδων πραγματικών αριθμών και ορίσαμε δύο πράξεις:
-άδων πραγματικών αριθμών και ορίσαμε δύο πράξεις:Είδαμε τις βασικές ιδιότητες που ικανοποιούν οι πράξεις αυτές.
Είδαμε το σύνολο των
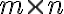 (
(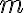 επί
επί 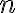 ) πινάκων
) πινάκων 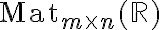 . Ένας
. Ένας 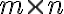 πίνακας είναι μία διάταξη αριθμών σε
πίνακας είναι μία διάταξη αριθμών σε 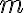 γραμμές και
γραμμές και 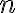 στήλες.
στήλες.
Συνήθως θα περιγράφουμε ένα τέτοιο πίνακα δίνοντας τα στοιχεία του
δίνοντας τα στοιχεία του 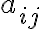 για
για 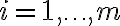 ,
, 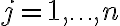 .
.
Oρίσαμε δύο πράξεις αντίστοιχες με αυτές του :
:Είδαμε ότι οι πράξεις της πρόσθεσης πινάκων και του πολλαπλασιασμού αριθμού με πίνακα ικανοποιούν τις ίδιες ιδιότητες με τις αντίστοιχες πράξεις του
 .
.Ορίσαμε τον πολλαπλασιασμό πινάκων. Ειδικότερα, όταν
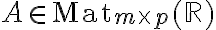 και
και 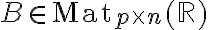 , (δηλαδή το πλήθος στηλών του
, (δηλαδή το πλήθος στηλών του  είναι ίσο με το πλήθος γραμμών του
είναι ίσο με το πλήθος γραμμών του 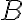 ) τότε ορίζεται το γινόμενο
) τότε ορίζεται το γινόμενο 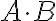 , το οποίο είναι ένας
, το οποίο είναι ένας 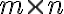 πίνακας. To
πίνακας. To 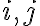 στοιχείο του πίνακα
στοιχείο του πίνακα 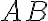 είναι το
είναι τοΟρίσαμε τις έννοιες του άνω (κάτω) τριγωνικού πίνακα, του διαγώνιου πίνακα, του συμμετρικού πίνακα.
Είδαμε βασικές ιδιότητες του πολλαπλασιασμού πινάκων. Ορίσαμε πότε ένας τετραγωνικός πίνακας είναι αντιστρέψιμος.
Αρχίσαμε να μελετάμε την έννοια της αντιστρεψιμότητας πινάκων. Είπαμε, χωρίς να το δικαιολογήσουμε, ότι για να είναι ένας πίνακας
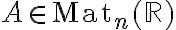 αντιστρέψιμος αρκεί να υπάρχει πίνακας
αντιστρέψιμος αρκεί να υπάρχει πίνακας 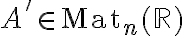 τέτοιος ώστε
τέτοιος ώστε 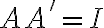 . Αν συμβαίνει αυτό, τότε είναι βέβαιο ότι θα ισχύει και
. Αν συμβαίνει αυτό, τότε είναι βέβαιο ότι θα ισχύει και 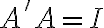 και άρα ο
και άρα ο  είναι αντιστρέψιμος. Δείξαμε ότι αν δύο πίνακες
είναι αντιστρέψιμος. Δείξαμε ότι αν δύο πίνακες 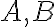 είναι αντιστρέψιμοι τότε το γινόμενο
είναι αντιστρέψιμοι τότε το γινόμενο 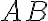 είναι αντιστρέψιμος πίνακας. Σε αυτή την περίπτωση ισχύει
είναι αντιστρέψιμος πίνακας. Σε αυτή την περίπτωση ισχύει 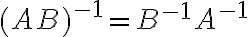 . Γενικότερα, αν οι πίνακες
. Γενικότερα, αν οι πίνακες 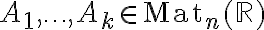 είναι αντιστρέψιμοι, τότε και ο πίνακας
είναι αντιστρέψιμοι, τότε και ο πίνακας  είναι αντιστρέψιμος και ισχύει
είναι αντιστρέψιμος και ισχύει 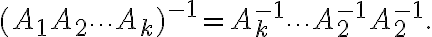
Αρχίσαμε να μιλάμε για απαλοιφή Gauss για τη λύση γραμμικών συστημάτων.
Διαβάστε: παρ. 2.1 από το βιβλίο [2].