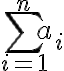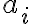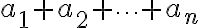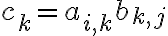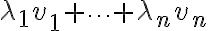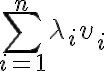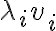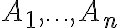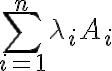Καλησπέρα Μαρία,
με βάση όσα έχουμε δει μέχρι τώρα, μπορούμε να γράψουμε στη μορφή αθροίσματος ένα συγκεκριμένο στοιχείο ενός πίνακα, ο οποίος προκύπτει από τον πολλαπλασιασμό δύο άλλων πινάκων. Ένας ολόκληρος τέτοιος πίνακας δεν γράφεται σε μορφή αθροίσματος, αλλά μπορούμε να δούμε ότι θα αποτελείται από αθροίσματα (καθώς μπορούμε να γράψουμε κάθε ένα από τα στοιχεία του ως άθροισμα).
Στο συνημμένο αρχείο έχω ένα γενικό παράδειγμα για 3x3 πίνακες. Τα ίδια θα ισχύουν και γενικότερα, για mxn πίνακες. Αν έχεις κι άλλες απορίες, μη διστάσεις να ρωτήσεις. Ελπίζω να σε βοήθησα!