Καλησπέρα. Θα ήθελα αν γίνεται να μου εξηγήσετε, γιατί οι μη μηδενικές γραμμές του U πίνακα είναι γραμμικώς ανεξάρτητες, όπως αναφέρεται στην τελευταία πρόταση του 2ου βίντεο, της 6ησ διάλεξης.
Πες ότι ο πίνακας 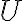 έχει
έχει 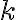 μη μηδενικές γραμμές, τις
μη μηδενικές γραμμές, τις 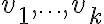 . Κάθε μία από αυτές έχει οδηγό. Ας ονομάσουμε
. Κάθε μία από αυτές έχει οδηγό. Ας ονομάσουμε 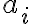 τον οδηγό της γραμμής
τον οδηγό της γραμμής 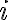 και ας πούμε ότι βρίσκεται στη στήλη
και ας πούμε ότι βρίσκεται στη στήλη 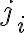 . Παρατηρήστε ότι κάτω από κάθε οδηγό έχουμε μηδενικά. Ας πάρουμε τώρα ένα γραμμικό συνδασμό
. Παρατηρήστε ότι κάτω από κάθε οδηγό έχουμε μηδενικά. Ας πάρουμε τώρα ένα γραμμικό συνδασμό 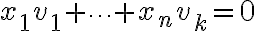 . Ποιά είναι η
. Ποιά είναι η 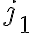 συνιστώστα του
συνιστώστα του 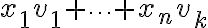 ; Είναι ίση με
; Είναι ίση με 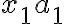 . Όμως όλες οι συνιστώσες του
. Όμως όλες οι συνιστώσες του 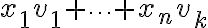 είναι ίσες με 0. Και
είναι ίσες με 0. Και 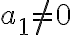 , άρα
, άρα 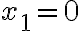 . Ποιά είναι η συνιστώσα
. Ποιά είναι η συνιστώσα 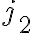 ; Είναι ίση με
; Είναι ίση με 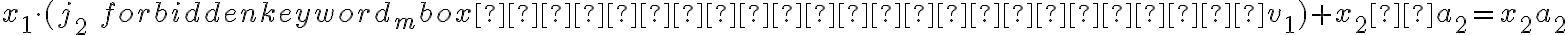 . Και
. Και 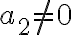 , άρα
, άρα 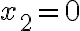 . Γενικά, η
. Γενικά, η 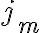 συνιστώσα του
συνιστώσα του 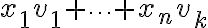 είναι ίση με
είναι ίση με
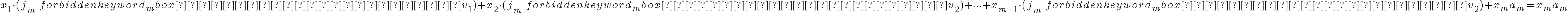
διότι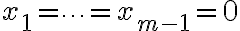 . Και
. Και 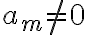 , άρα
, άρα 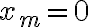 .
.
Έτσι όλοι οι συντελεστές πρέπει να είναι ίσοι με 0, άρα τα διανύσματα είναι γραμμικώς ανεξάρτητα.
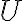 έχει
έχει 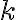 μη μηδενικές γραμμές, τις
μη μηδενικές γραμμές, τις 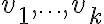 . Κάθε μία από αυτές έχει οδηγό. Ας ονομάσουμε
. Κάθε μία από αυτές έχει οδηγό. Ας ονομάσουμε 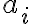 τον οδηγό της γραμμής
τον οδηγό της γραμμής 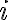 και ας πούμε ότι βρίσκεται στη στήλη
και ας πούμε ότι βρίσκεται στη στήλη 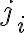 . Παρατηρήστε ότι κάτω από κάθε οδηγό έχουμε μηδενικά. Ας πάρουμε τώρα ένα γραμμικό συνδασμό
. Παρατηρήστε ότι κάτω από κάθε οδηγό έχουμε μηδενικά. Ας πάρουμε τώρα ένα γραμμικό συνδασμό 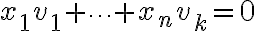 . Ποιά είναι η
. Ποιά είναι η 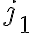 συνιστώστα του
συνιστώστα του 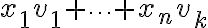 ; Είναι ίση με
; Είναι ίση με 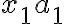 . Όμως όλες οι συνιστώσες του
. Όμως όλες οι συνιστώσες του 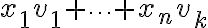 είναι ίσες με 0. Και
είναι ίσες με 0. Και 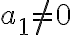 , άρα
, άρα 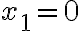 . Ποιά είναι η συνιστώσα
. Ποιά είναι η συνιστώσα 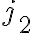 ; Είναι ίση με
; Είναι ίση με 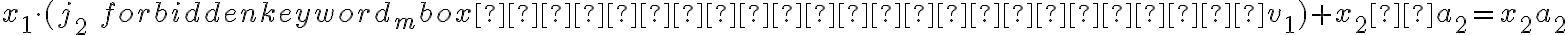 . Και
. Και 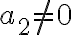 , άρα
, άρα 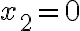 . Γενικά, η
. Γενικά, η 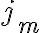 συνιστώσα του
συνιστώσα του 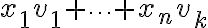 είναι ίση με
είναι ίση με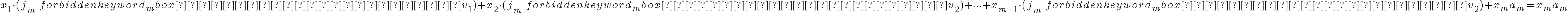
διότι
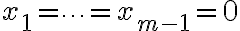 . Και
. Και 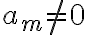 , άρα
, άρα 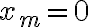 .
.Έτσι όλοι οι συντελεστές πρέπει να είναι ίσοι με 0, άρα τα διανύσματα είναι γραμμικώς ανεξάρτητα.
Ευχαριστώ!!

