Καλημέρα σας , θα ήθελα να μου εξηγήσετε γιατί το άθροισμα <(1,0,0)>+<(0,1,0)> είναι ευθύ και γιατί ισχυει το εξής
Αν vε<(1,0,0)>U<(0,1,0)> τοτε v=x(1,0,0)=y(0,1,0)?
Καλημέρα σας , θα ήθελα να μου εξηγήσετε γιατί το άθροισμα <(1,0,0)>+<(0,1,0)> είναι ευθύ και γιατί ισχυει το εξής
Αν vε<(1,0,0)>U<(0,1,0)> τοτε v=x(1,0,0)=y(0,1,0)?
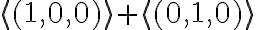 είναι ευθύ, διότι
είναι ευθύ, διότι 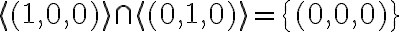 . Πραγματικά, εάν
. Πραγματικά, εάν 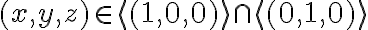 , τότε
, τότε 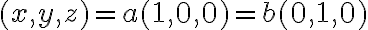 , που συνεπάγεται ότι
, που συνεπάγεται ότι 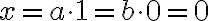 , οπότε
, οπότε 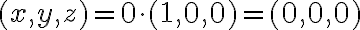 .
. 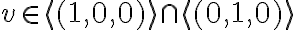 , τότε
, τότε 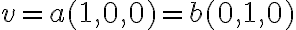 για κάποια
για κάποια 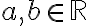 . Η ισότητα
. Η ισότητα 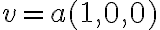 προκύπτει από το
προκύπτει από το 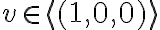 . Η ισότητα
. Η ισότητα 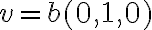 προκύπτει από το
προκύπτει από το 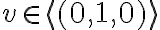 . Αφού το
. Αφού το 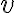 ανήκει στην τομή των δύο υπόχωρων θα ανήκει σε καθένα από αυτούς.
ανήκει στην τομή των δύο υπόχωρων θα ανήκει σε καθένα από αυτούς.