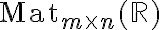Section outline

  • Έγινε μια εισαγωγή στον χώρο των γραμμικών απεικονίσεων. Είδαμε τον ορισμό και τον χαρακτηρισμό μιας γραμμικής απεικόνισης 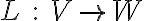\(L \ : \ V\to W\) και τις αντίστοιχες βασικές προτάσεις και ιδιότητες, είδαμε παραδείγματα γραμμικών απεικονίσεων, είδαμε μια αντιστοιχία ανάμεσα στους 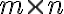\(m\times n\) πραγματικούς πίνακες και τις γραμμικές απεικονίσεις 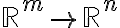\(\mathbb{R}^m\to\mathbb{R}^n\). Στην συνέχεια ορίσαμε τον πυρήνα και την εικόνα μιας γραμμικής απεικόνισης, δείξαμε ότι πρόκειται για υπόχωρους και δείξαμε ότι αν 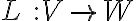\(L \ : V\to W\), τότε 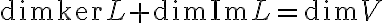\(\mathrm{dim}\mathrm{ker}L + \mathrm{dim}\mathrm{Im}L = \mathrm{dim} V\). Τέλος, δείξαμε ότι κάθε γραμμική απεικόνιση 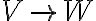\(V\to W\) χαρακτηρίζεται πλήρως από την απεικόνιση των στοιχείων μιας βάσης του \(V\).

    Αναρτήθηκε το 9ο φυλλάδιο ασκήσεων.

    Μελετήστε την παράγραφο 7.1 από το σύγγραμμα [1].