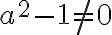Καλησπέρα σας!
Θα μπορούσατε να μου εξηγήσετε την στρατηγική επίλυσης αυτών των δύο ασκήσεων παρακάτω;
--- Στην πρώτη, έκανα απαλοιφή Gauss στον πίνακα που μας δίνετε, εκτελώντας τις γραμμοπράξεις:
1) Γ2 ← Γ2 - Γ1 και 2) Γ3 ← Γ3 + Γ2 και κατέληξα στον κλιμακωτό πίνακα U:
1 1 -1 1
0 -2 α2 -2
0 0 α2 - 2α α2 - 2
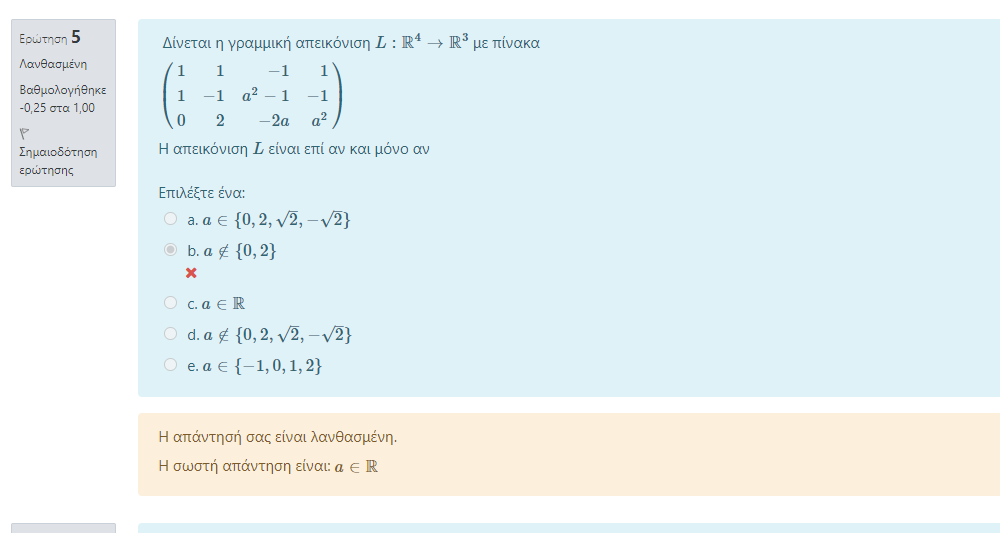
Μετά σκέφτηκα ότι για να είναι η απεικόνιση L επί, θα πρέπει: Im(L) = W = ℝ3
Άρα θα πρέπει dim(ImL) = dim(W) = dim(ℝ3) = 3 άρα rank(L) = 3 = τάξη πίνακα
και συνεπώς θέλουμε ο πίνακας να έχει τάξη 3 άρα θα πρέπει να έχει 3 οδηγούς άρα
θα πρέπει α2 - 2α ≠ 0 ⇔ α∉{0,2} και α2 - 2 ≠ 0 δηλαδή το α να μην είναι ρίζα 2 και πλην ρίζα 2
Πως προέκυψε το ότι α∈ℝ ;
--- Στην δεύτερη δεν κατάλαβα τι πρέπει να κάνω για να την λύσω

Ευχαριστώ πολύ για τον χρόνο σας!