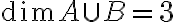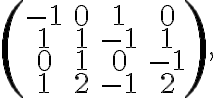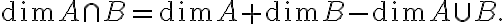ΑΣΚΗΣΗ ΠΡΟΟΔΟΥ

ΑΣΚΗΣΗ ΠΡΟΟΔΟΥ

by ΣΤΥΛΙΑΝΟΣ ΜΑΝΟΥΣΕΛΗΣ -
Number of replies: 1

Κύριε καλησπέρα σας ! Ήθελα να ρωτήσω κάτι σχετικά με μια άσκηση της 2ης Προόδου που γράψαμε. Συγκεκριμένα είναι η άσκηση με την εκφώνηση :

"Η διάσταση του χώρου ⟨(−1,0,1,0),(1,1,−1,1)⟩∩⟨(0,1,0,−1),(1,2,−1,2)⟩⟨(−1,0,1,0),(1,1,−1,1)⟩∩⟨(0,1,0,−1),(1,2,−1,2)⟩ είναι ίση με......" 

δίνοντας κάποιες επιλογές, και κάνοντας εγώ ξανά τις πράξεις βγάζω ότι έχει διάσταση 2. Μπορείτε να μου εξηγήσετε πως βγαίνει ; 

Σας ευχαριστώ πολύ !!!

In reply to ΣΤΥΛΙΑΝΟΣ ΜΑΝΟΥΣΕΛΗΣ

Απάντηση: ΑΣΚΗΣΗ ΠΡΟΟΔΟΥ

by ΓΕΩΡΓΙΟΣ ΚΑΠΕΤΑΝΑΚΗΣ -
Γεια σου Στέλιο,
Η σωστή απάντηση είναι 1. Ένας τρόπος να το δεις (δεν είναι ο μοναδικός), είναι ο εξής: Μπορείς να δεις ότι \dim A\cup B = 3, υπολογίζοντας την διάσταση του χώρου γραμμών του πίνακα \begin{pmatrix} -1&0&1&0 \\ 1&1&-1&1 \\ 0&1&0&-1 \\ 1&2&-1&2 \end{pmatrix} , η οποία με την βοήθεια της απαλοιφής Gauss βγαίνει 3. Το αποτέλεσμα προκύπτει από την σχέση
\dim A\cap B = \dim A + \dim B - \dim A\cup B .