Καλησπερα! Παρατηρησα οτι στο τελος της ασκησης 8,9 χρησιμοποιουμε οτι η ταξη του πινακα ειναι ιση με την ταξη του αναστροφου. Μπορειτε να μου εξηγησετε γιατι ισχυει αυτο? Ευχαριστω εκ των προτερων!!
Ορίσαμε την τάξη, 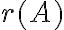 , του πίνακα
, του πίνακα  να είναι το πλήθος των οδηγών του κλιμακωτού πίνακα,
να είναι το πλήθος των οδηγών του κλιμακωτού πίνακα, 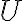 , στον οποίο καταλήγουμε με την απαλοιφή Gauss και έχουμε δείξει ότι είναι ίση με τη διάσταση του χώρου στηλών του. Δηλαδή
, στον οποίο καταλήγουμε με την απαλοιφή Gauss και έχουμε δείξει ότι είναι ίση με τη διάσταση του χώρου στηλών του. Δηλαδή 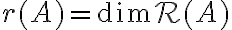 . Παρατηρήστε τώρα, ότι κάθε μη μηδενική γραμμή του
. Παρατηρήστε τώρα, ότι κάθε μη μηδενική γραμμή του 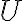 έχει ακριβώς ένα οδηγό και το σύνολο των μη μηδενικών γραμμών είναι βάση του χώρου γραμμών του
έχει ακριβώς ένα οδηγό και το σύνολο των μη μηδενικών γραμμών είναι βάση του χώρου γραμμών του 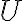 , αλλά και του αρχικού πίνακα
, αλλά και του αρχικού πίνακα  . Οπότε η διάσταση του χώρου γραμμών του
. Οπότε η διάσταση του χώρου γραμμών του  είναι επίσης ίση με την τάξη του. Δηλαδή
είναι επίσης ίση με την τάξη του. Δηλαδή 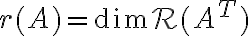 . Όμως, όπως είπαμε,
. Όμως, όπως είπαμε, 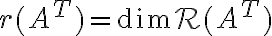 . Άρα
. Άρα 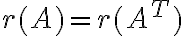 .
.
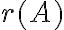 , του πίνακα
, του πίνακα  να είναι το πλήθος των οδηγών του κλιμακωτού πίνακα,
να είναι το πλήθος των οδηγών του κλιμακωτού πίνακα, 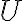 , στον οποίο καταλήγουμε με την απαλοιφή Gauss και έχουμε δείξει ότι είναι ίση με τη διάσταση του χώρου στηλών του. Δηλαδή
, στον οποίο καταλήγουμε με την απαλοιφή Gauss και έχουμε δείξει ότι είναι ίση με τη διάσταση του χώρου στηλών του. Δηλαδή 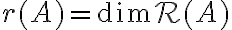 . Παρατηρήστε τώρα, ότι κάθε μη μηδενική γραμμή του
. Παρατηρήστε τώρα, ότι κάθε μη μηδενική γραμμή του 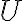 έχει ακριβώς ένα οδηγό και το σύνολο των μη μηδενικών γραμμών είναι βάση του χώρου γραμμών του
έχει ακριβώς ένα οδηγό και το σύνολο των μη μηδενικών γραμμών είναι βάση του χώρου γραμμών του 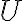 , αλλά και του αρχικού πίνακα
, αλλά και του αρχικού πίνακα  . Οπότε η διάσταση του χώρου γραμμών του
. Οπότε η διάσταση του χώρου γραμμών του  είναι επίσης ίση με την τάξη του. Δηλαδή
είναι επίσης ίση με την τάξη του. Δηλαδή 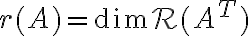 . Όμως, όπως είπαμε,
. Όμως, όπως είπαμε, 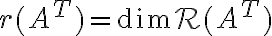 . Άρα
. Άρα 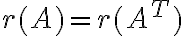 .
.Οκ καταλαβα. Ευχαριστω!!!

