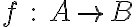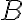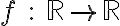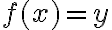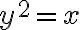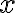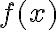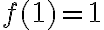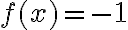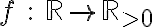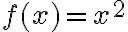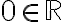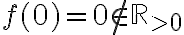- Να είναι μονοσήμαντα ορισμένη, δηλαδή για δεδομένο
 να μπορώ να βρώ κάποιο
να μπορώ να βρώ κάποιο 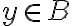 τέτοιο ώστε
τέτοιο ώστε 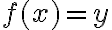 , αλλά ταυτόχρονα αυτό το
, αλλά ταυτόχρονα αυτό το 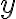 να είναι μοναδικό, δηλαδή να μην μπορώ να βρω
να είναι μοναδικό, δηλαδή να μην μπορώ να βρω 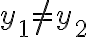 με
με 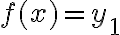 και
και 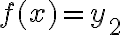 .
. - Για κάθε
 να ισχύει ότι
να ισχύει ότι 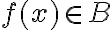 .
.
Συνήθως και τα δύο είναι προφανή, οπότε δεν χρειάζεται να ασχοληθούμε με το ζήτημα, όμως μερικές φορές μπορεί να μην είναι. Ας δούμε παραδείγματα πραγματικών συναρτήσεων (που είμαστε πιο εξοικειωμένοι) που δεν είναι καλά ορισμένες: