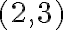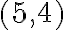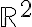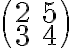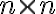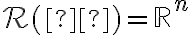Στις σημειώσεις του κύριου Κουρουνιώτη, στη σελίδα 104, στο παράδειγμα 6.11 θα ήθελα να ρωτήσω κάτι. Σχετικά με αυτό που αναφέρει το παράδειγμα, αν εγώ πάρω έναν πίνακα έστω 2x2, ας πούμε τον πίνακα που έχει για στήλες τα διανύσματα (2,3) και (5,4) και ο οποίος είναι αντιστρέψιμος, τότε μπορώ να πω πως τα διανύσματα (2,3) και (5,4) είναι βάση του ℝn. Αλλά αν τύχαινε και ο πίνακας δεν ήταν αντιστρέψιμος, τότε δεν θα αποτελούσαν βάση τα διανύσματα των στηλών του;
Σωστά. Τα 
και 
είναι βάση του 
και αυτό είναι ισοδύναμο με το ότι ο πίνακας 
είναι αντιστρέψιμος, αλλά αν ο αντίστοιχος πίνακας δεν ήταν αντιστρέψιμος δεν θα ήταν.
και είναι βάση του και αυτό είναι ισοδύναμο με το ότι ο πίνακας είναι αντιστρέψιμος, αλλά αν ο αντίστοιχος πίνακας δεν ήταν αντιστρέψιμος δεν θα ήταν.Παρατήρησε ότι οι στήλες ενός 
πίνακα είναι βάση του 
αν και μόνο αν 
. Το τελευταίο ισχύει αν και μόνο αν ο πίνακας έχει τάξη ίση με 
. Ισοδύναμα δηλαδή αν και μόνο αν ο πίνακας είναι αντιστρέψιμος.
πίνακα είναι βάση του αν και μόνο αν . Το τελευταίο ισχύει αν και μόνο αν ο πίνακας έχει τάξη ίση με . Ισοδύναμα δηλαδή αν και μόνο αν ο πίνακας είναι αντιστρέψιμος.