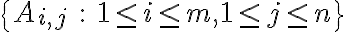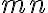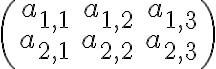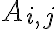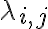Βάση ενός χώρου V

Βάση ενός χώρου V

από ΓΕΩΡΓΙΟΣ ΓΙΑΝΝΟΥΛΑΚΗΣ -
Αριθμός απαντήσεων: 2

Μπορείτε να μου εξηγήσετε πώς θα αποδείξω ότι το σύνολο Ai,j (όπου ο Α έχει 1 στη θέση i,j και 0 στις υπόλοιπες θέσεις) παράγει τον χώρο Mat2x3(ℝ) ; Δεν αρκεί να δείξω ότι οι 6 πίνακες Ai,j (δηλαδή οι Α1,1 , Α1,2 , Α1,3 , Α2,1 , Α2,2 , Α2,3) είναι γραμμικώς ανεξάρτητοι;

Αφού ούτως ή άλλως το να δείξω ότι ⟨Ai,j⟩ = Mat2x3(ℝ) είναι ισοδύναμο με το να αποδείξω ότι οι 6 πίνακες που προανέφερα είναι γραμμικώς ανεξάρτητοι. Ή κάνω κάποιο λάθος σε αυτόν μου τον συλλογισμό ;

Ευχαριστώ πολύ για τον χρόνο σας

Σε απάντηση σε ΓΕΩΡΓΙΟΣ ΓΙΑΝΝΟΥΛΑΚΗΣ

Απάντηση: Βάση ενός χώρου V

από Θεόδουλος Γαρεφαλάκης -
Θα αρκούσε να δείξεις ότι το σύνολο \{A_{i,j}\ :\ 1\leq i\leq m, 1\leq j\leq n\} είναι γραμμικώς ανεξάρτητο, εάν ήξερες ότι ο χώρος έχει διάσταση mn. Όμως αυτό θέλεις να δείξεις. Οπότε πρέπει να δείξεις ότι το σύνολο αυτό είναι βάση, δηλαδή ότι είναι γραμμικώς ανεξάρτητο και ότι παράγει το χώρο. Δείξε και τις δύο ιδότητες. Σχετικά με την παραγωγή: θέλεις να δείξεις ότι κάθε πίνακας
\left(\begin{array}{rrr}a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3}\end{array}\right)
μπορεί να γραφεί ως γραμμικός συνδυασμός των A_{i,j}. Βάλε συντελεστή \lambda_{i,j} στον πίνακα A_{i,j} και δείξε ότι τέτοιοι συντελεστές υπάρχουν. Μπορείς (εύκολα) να τους υπολογίσεις.