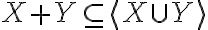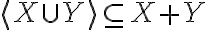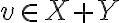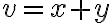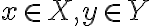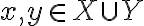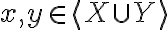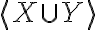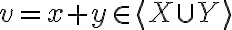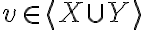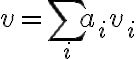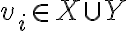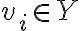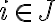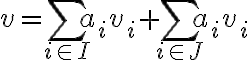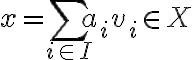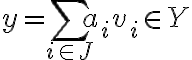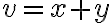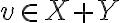Καλησπέρα σας
Δυσκολεύομαι να καταλάβω την λογική της απόδειξης του εξής θεωρήματος:
" Το άθροισμα των διανυσματικών υπόχωρων X + Y είναι διανυσματικός υπόχωρος του V, και παράγεται από την ένωση X ∪ Y, δηλαδή X + Y = ⟨X ∪ Y⟩ "
Μήπως θα μπορούσατε να μου την εξηγήσετε λίγο πιο αναλυτικά ;
Ευχαριστώ πολύ!