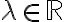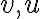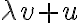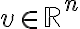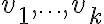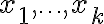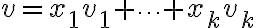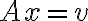Γειά σας
Μπορείτε να μου εξηγήσετε αναλυτικά πως λύνεται η άσκηση με τα διανύσματα που ανήκουν στον χώρο που δίνεται, του δοκιμαστικού τεστ;
Επιπλέον έχω λίγο μπερδευτεί με το πως αποδεικνύουμε ότι ένα σύνολο είναι υπόχωρος ενός διανυσματικού χώρου.
Εφαρμόζουμε το κριτήριο του υπόχωρου με ποιον τρόπο; Παίρνουμε απλά τυχαίο πολλαπλάσιο (λ) και αποδεικνύουμε ότι λv + u ανήκει επίσης στον χώρο που μας δίνεται;
Ευχαριστώ πολύ