11 May - 17 May
Section outline
-
Δείξαμε ότι το δυναμοσύνολο
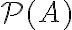 ενός συνόλου
ενός συνόλου  έχει αυστηρά μεγαλύτερο πληθάριθμο από το σύνολο
έχει αυστηρά μεγαλύτερο πληθάριθμο από το σύνολο  . Δηλαδή, υπάρχει απεικόνιση
. Δηλαδή, υπάρχει απεικόνιση 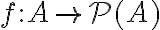 η οποία είναι 1-1, αλλά δεν υπάρχει απεικόνιση
η οποία είναι 1-1, αλλά δεν υπάρχει απεικόνιση 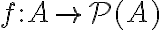 η οποία είναι επί. Στη συνέχεια είδαμε ότι ο πληθάριθμος του συνόλου
η οποία είναι επί. Στη συνέχεια είδαμε ότι ο πληθάριθμος του συνόλου 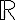 των πραγματικών αριθμών είναι ίσος με τον πληθάριθμο του δυναμοσυνόλου
των πραγματικών αριθμών είναι ίσος με τον πληθάριθμο του δυναμοσυνόλου 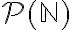 των φυσικών. Αυτό και η παραπάνω πρόταση μας δίνουν σαν συμπέρασμα ότι ο πληθάριθμος των πραγματικών αριθμών είναι αυστηρά μεγαλύτερος από τον πληθάριθμο των φυσικών: οι πραγματικοί αριθμοί δεν είναι αριθμήσιμο σύνολο. Η ίδια απόδειξη μπορεί να γίνει και με το διαγώνιο επιχείρημα του Cantor, που επίσης είδαμε.
των φυσικών. Αυτό και η παραπάνω πρόταση μας δίνουν σαν συμπέρασμα ότι ο πληθάριθμος των πραγματικών αριθμών είναι αυστηρά μεγαλύτερος από τον πληθάριθμο των φυσικών: οι πραγματικοί αριθμοί δεν είναι αριθμήσιμο σύνολο. Η ίδια απόδειξη μπορεί να γίνει και με το διαγώνιο επιχείρημα του Cantor, που επίσης είδαμε.Διαβάστε: σελ. 125-129 από τις σημειώσεις Χ. Κουρουνιώτη

