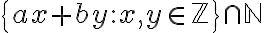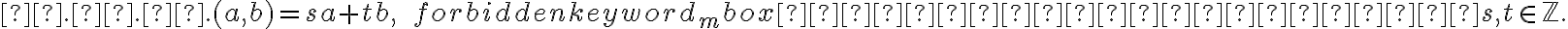Section outline

  • Μιλήσαμε για την Αρχή της Επαγωγής και είδαμε κάποια παραδείγματα.

    Είδαμε την Ισχυρή Επαγωγή και δείξαμε ότι ως αποδεικτική μέθοδος (αν και συχνά βολική) δεν είναι πραγματικά ισχυρότερη από την "απλή" επαγωγή. Ειδικότερα, δείξαμε ότι προκύπτει από την Αρχή της Επαγωγής.

    Είδαμε την Αρχή του Ελαχίστου. Την αποδείξαμε με επαγωγή (ισχυρή). Είδαμε κάποια παραδείγματα.

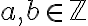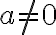    Ορίσαμε το μέγιστο κοινό διαιρέτη δύο ακεραίων και δείξαμε ότι υπάρχει, αρκεί να μην είναι και οι δύο ίσοι με το 0. Δείξαμε ότι για a,b\in \mathbb{Z} με a\neq 0, το σύνολο 

    \left\{a x + b y : x,y \in \mathbb{Z}\right\} \cap \mathbb{N}

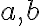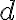    έχει ελάχιστο στοιχείο, το οποίο είναι μεγιστος κοινός διαιρέτης των a,b. Αν d είναι ένας μ.κ.δ. των 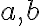a,b, τότε και το 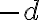-d είναι επίσης ένας μ.κ.δ. Για να κάνουμε το μ.κ.δ. μοναδικό, παίρνουμε τον θετικό από τους δύο αριθμούς. Η απόδειξη αυτή μας δίνει επιπλέον, ότι ο

    \text{μ.κ.δ.}(a, b) = s a + t b,\ \ \mbox{ για κάποιους } s,t \in \mathbb{Z}.

    Μιλήσαμε για πρώτους αριθμούς και δείξαμε ότι είναι άπειροι. Δείξαμε ότι κάθε αριθμός γράφεται ως γινόμενο πρώτων.

    Διαβάστε: σελ. 97-98 από τις σημειώσεις Χ. Κουρουνιώτη.

    Διαβάστε: σελ. 98-101 από τις σημειώσεις Χ. Κουρουνιώτη.