καλησπερα σας θα μπορουσατ να μου εξηγησετε την απεικονιση επι και την 1-1 και πως ουσιαστικα τις χρησιμοποιουμε
Σας ευχαριστω εκ των πρωτερον
καλησπερα σας θα μπορουσατ να μου εξηγησετε την απεικονιση επι και την 1-1 και πως ουσιαστικα τις χρησιμοποιουμε
Σας ευχαριστω εκ των πρωτερον
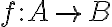 ονομάζεται 1-1 αν διαφορετικά στοιχεία του
ονομάζεται 1-1 αν διαφορετικά στοιχεία του  απεικονίζονται σε διαφορετικά στοιχεία του
απεικονίζονται σε διαφορετικά στοιχεία του 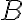 . Δηλαδή
. Δηλαδή 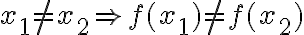 . Η
. Η  ονομάζεται επί αν κάθε στοιχείο του
ονομάζεται επί αν κάθε στοιχείο του 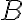 είναι εικόνα κάποιου στοιχείου του
είναι εικόνα κάποιου στοιχείου του  κάτω από την
κάτω από την  . Δηλαδή αν για κάθε
. Δηλαδή αν για κάθε 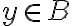 υπάρχει
υπάρχει  τέτοιο ώστε
τέτοιο ώστε 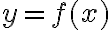 . Ισοδύναμα, αν
. Ισοδύναμα, αν 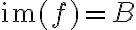 .
.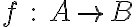 είναι 1-1 αν για κάθε στοιχείο
είναι 1-1 αν για κάθε στοιχείο 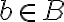 έχεις το πολύ ένα στοιχείο
έχεις το πολύ ένα στοιχείο 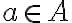 τέτοιο ώστε
τέτοιο ώστε 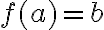 . Με άλλα λόγια δεν υπάρχουν δυο στοιχεία του
. Με άλλα λόγια δεν υπάρχουν δυο στοιχεία του  που να απεικονίζονται στο ίδιο
που να απεικονίζονται στο ίδιο 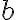 .
.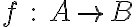 είναι επί αν για κάθε στοιχείο
είναι επί αν για κάθε στοιχείο 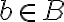 έχεις τουλάχιστον ένα στοιχείο
έχεις τουλάχιστον ένα στοιχείο 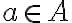 τέτοιο ώστε
τέτοιο ώστε 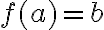 . Με άλλα λόγια η
. Με άλλα λόγια η  πιάνει ολόκληρο το
πιάνει ολόκληρο το 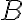 .
.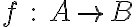 είναι 1-1 και επί αν για κάθε στοιχείο
είναι 1-1 και επί αν για κάθε στοιχείο 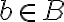 έχεις ακριβώς ένα στοιχείο
έχεις ακριβώς ένα στοιχείο 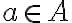 τέτοιο ώστε
τέτοιο ώστε 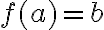 . Αυτό σημαίνει ότι τότε έχουμε μια απόλυτη αντιστοιχία, η οποία μάλιστα μπορεί να δουλέψει και αντίστροφα (για αυτό και αυτές οι απεικονίσεις είναι αντιστρέψιμες).
. Αυτό σημαίνει ότι τότε έχουμε μια απόλυτη αντιστοιχία, η οποία μάλιστα μπορεί να δουλέψει και αντίστροφα (για αυτό και αυτές οι απεικονίσεις είναι αντιστρέψιμες).