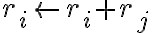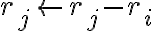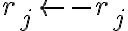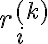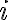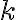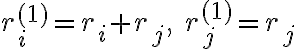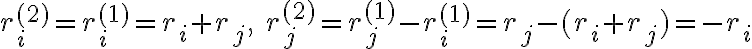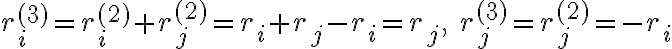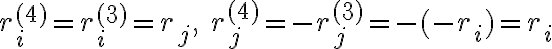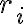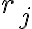Άσκηση 4.1.β

Άσκηση 4.1.β

by ΕΙΡΗΝΗ ΦΑΛΙΑΚΑΚΗ -
Number of replies: 1

Στο συγκεκριμένο ερώτημα στις πράξεις που κάνω στο δεξί μέλος καταλήγω ότι ri<-- ri-rj, δεν μπορώ να καταλάβω όμως πως μπορώ να αποδείξω ότι αυτό είναι ίσο με το αριστερό μέλος Pi,j**-1, το οποίο γνωρίζω ότι είναι ίσο με Pi,j.

In reply to ΕΙΡΗΝΗ ΦΑΛΙΑΚΑΚΗ

Απάντηση: Άσκηση 4.1.β

by ΓΕΩΡΓΙΟΣ ΚΑΠΕΤΑΝΑΚΗΣ -

Γεια σου Ειρήνη,

Στο δεξί μέρος έχουμε διαδοχικά τις εξής πράξεις γραμμών:
  1. r_i \leftarrow r_i+r_j
  2. r_j \leftarrow r_j - r_i
  3. r_i \leftarrow r_i+r_j
  4. r_j \leftarrow -r_j

Θα συμβολίζω με r_i^{(k)} την i-στή γραμμή μετά το k-στό βήμα. Έτσι έχουμε:

  1. r_i^{(1)} = r_i + r_j , \ r_j^{(1)} = r_j
  2. r_i^{(2)} = r_i^{(1)} = r_i+r_j , \ r_j^{(2)} = r_j^{(1)} - r_i^{(1)} = r_j - (r_i+r_j) = -r_i
  3. r_i^{(3)} = r_i^{(2)} + r_j^{(2)} = r_i+r_j-r_i = r_j , \ r_j^{(3)} = r_j^{(2)} = -r_i
  4. r_i^{(4)} = r_i^{(3)} = r_j , \ r_j^{(4)} = -r_j^{(3)} = -(-r_i) = r_i

Επομένως παρατηρούμε ότι στο τέλος ουσιαστικά έχουμε εναλλάξει τις γραμμές r_i και r_j.