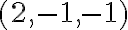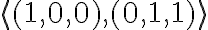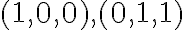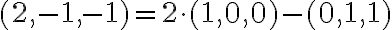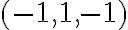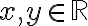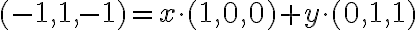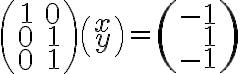δοκιμαστικο τεστ

δοκιμαστικο τεστ

by ΜΑΡΙΝΑ ΡΑΜΑ -
Number of replies: 3

στην 1η ερωτηση γιατι  το διαωυσμα (2,-1,-1) ανηκει στον χωρο<(1,0,0),(0,1,1) και οχι το (-1,1,-1)

In reply to ΜΑΡΙΝΑ ΡΑΜΑ

Απάντηση: δοκιμαστικο τεστ

by ΝΙΚΗ ΣΠΙΘΑΚΗ -
Για να εξετάσεις αν κάποιο διάνυσμα ανήκει στο χώρο που παράγεται από ένα πεπερασμένο πλήθος διανυσμάτων, θα πρέπει να δεις αν το αρχικό διάνυσμα μπορεί να γραφτεί σαν γραμμικός συνδυασμός των διανυσμάτων που παράγουν το χώρο με συντελεστές πραγματικούς αριθμούς.

Στη συγκεκριμένη άσκηση, ψάχνουμε x1, x2 πραγματικούς αριθμούς τέτοιους ώστε

(2,-1,-1)=x1(1,0,0)+x2(0,1,1).

Εύκολα μπορούμε να δούμε ότι από το παραπάνω προκύπτει ένα σύστημα της μορφής Αx=b, όπου Α είναι ο πίνακας που έχει ως στήλες τα διανύσματα (1,0,0) και (0,1,1), x=(x1, x2) και b=(2,-1,-1) (γραμμένα ως διανύσματα-στήλες). Λύνοντας το σύστημα με τις μεθόδους που ξέρουμε, βρίσκουμε μία λύση x=(x1,x2). Επομένως, το (2,-1,-1) μπορεί να γραφτεί στην παραπάνω μορφή και άρα ανήκει στον <(1,0,0), (0,1,1)>.
Ακολουθούμε την ίδια διαδικασία για το (-1,1,-1) και βλέπουμε ότι το σύστημα που προκύπτει δεν έχει λύση. Επομένως, το διάνυσμα δεν μπορεί να γραφτεί ως γραμμικός συνδυασμός των (1,0,0) και (0,1,1) και άρα δεν ανήκει στο χώρο που παράγεται από αυτά.
In reply to ΜΑΡΙΝΑ ΡΑΜΑ

Απάντηση: δοκιμαστικο τεστ

by Θεόδουλος Γαρεφαλάκης -
Το διάνυσμα (2,-1,-1) ανήκει στο χώρο \langle (1,0,0), (0,1,1)\rangle διότι είναι γραμμικός συνδυασμός των (1,0,0), (0,1,1). Για παράδειγμα, (2,-1,-1) = 2\cdot (1,0,0) - (0,1,1). Αντίθετα, το (-1,1,-1) δεν μπορεί να γραφεί ως γραμμικός συνδυασμός των (1,0,0), (0,1,1). Αν γραφόταν, τότε θα υπήρχαν x,y\in\mathbb{R} τέτοιοι ώστε (-1,1,-1) = x\cdot (1,0,0) + y\cdot (0,1,1). Ισοδύναμα,
\left(\begin{array}{rr}1 & 0\\ 0 & 1\\ 0 & 1\end{array}\right) \left(\begin{array}{c}x\\y\end{array}\right) = \left(\begin{array}{r}-1\\1\\-1\end{array}\right)
Δείξτε ότι το παραπάνω σύστημα δεν έχει λύση.