Για να είναι το υποσύνολο 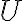 του γραμμικού χώρου
του γραμμικού χώρου  υπόχωρος πρέπει να είναι μη κενό και για κάθε
υπόχωρος πρέπει να είναι μη κενό και για κάθε 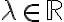 και κάθε
και κάθε 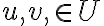 πρέπει να ισχύει
πρέπει να ισχύει 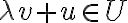 . Δεν επιλέγεις με κάποιο τρόπο τα
. Δεν επιλέγεις με κάποιο τρόπο τα 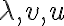 . Πρέπει να είναι τυχόντα. Το
. Πρέπει να είναι τυχόντα. Το 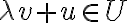 πρέπει να ισχύει για κάθε
πρέπει να ισχύει για κάθε 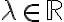 και για κάθε
και για κάθε 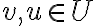 .
.
Για το σύνολο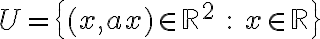 , παρατήρησε αρχικά ότι δεν είναι κενό (γιατί;) Ας πάρουμε ένα (οποιοδήποτε) πραγμτικό αριθμό
, παρατήρησε αρχικά ότι δεν είναι κενό (γιατί;) Ας πάρουμε ένα (οποιοδήποτε) πραγμτικό αριθμό 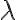 και δύο (οποιαδήποτε) στοιχεία του
και δύο (οποιαδήποτε) στοιχεία του 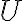 , ας πούμε τα
, ας πούμε τα 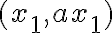 και
και 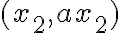 . Τότε
. Τότε
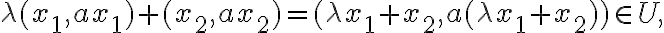
διότι είναι της μορφής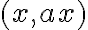 με
με 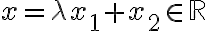 .
.
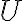 του γραμμικού χώρου
του γραμμικού χώρου  υπόχωρος πρέπει να είναι μη κενό και για κάθε
υπόχωρος πρέπει να είναι μη κενό και για κάθε 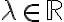 και κάθε
και κάθε 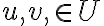 πρέπει να ισχύει
πρέπει να ισχύει 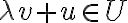 . Δεν επιλέγεις με κάποιο τρόπο τα
. Δεν επιλέγεις με κάποιο τρόπο τα 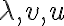 . Πρέπει να είναι τυχόντα. Το
. Πρέπει να είναι τυχόντα. Το 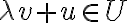 πρέπει να ισχύει για κάθε
πρέπει να ισχύει για κάθε 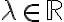 και για κάθε
και για κάθε 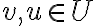 .
.Για το σύνολο
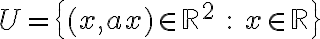 , παρατήρησε αρχικά ότι δεν είναι κενό (γιατί;) Ας πάρουμε ένα (οποιοδήποτε) πραγμτικό αριθμό
, παρατήρησε αρχικά ότι δεν είναι κενό (γιατί;) Ας πάρουμε ένα (οποιοδήποτε) πραγμτικό αριθμό 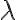 και δύο (οποιαδήποτε) στοιχεία του
και δύο (οποιαδήποτε) στοιχεία του 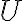 , ας πούμε τα
, ας πούμε τα 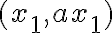 και
και 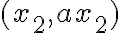 . Τότε
. Τότε 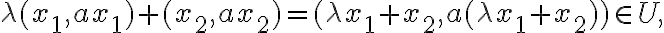
διότι είναι της μορφής
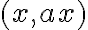 με
με 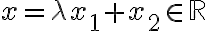 .
.
