Section outline

  • Αυτή την εβδομάδα συνεχίσαμε να μιλάμε για ιδιοτιμές και ιδιοδιανύσματα ενός πίνακα και είδαμε πότε ένας πίνακας είναι διαγωνίσιμος. Μιλήσαμε για αλγεβρική και γεωμετρική πολλαπλότητα ιδιοτιμών και είδαμε ότι για κάθε πίνακα Α και για κάθε ιδιοτιμή του λ η αλγεβρική πολλαπλότητα της λ  είναι μεγαλύτερη ή ίση της γεωμετρικής πολλαπλότητας της λ.

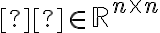    Είδαμε ότι ένας πίνακας Α \in \mathbb{R}^{n \times n} διαγωνιοποιείται αν και μόνο αν o 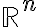\mathbb{R}^n έχει βάση ιδιοδιανυσμάτων του. Αν μάλιστα  το χαρακτηριστικό πολυώνυμο του Α  παραγοντοποιείται σαν γινόμενο πρωτοβάθμιων (με κάποιους εκθέτες) δηλ.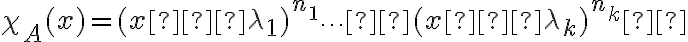 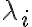 \chi_A(x)=(x−\lambda_1)^{n_1} \cdots (x−\lambda_k)^{n_k}  , τότε ο πίνακας Α διαγωνιοποιείται αν και μόνο αν η αλγεβρική πολ/τα της κάθε ιδιοτιμής \lambda_i ισούται με την αντίστοιχη γεωμετρική της πολ/τα.

    Τέλος είδαμε αρκετά παραδείγματα. 

    Διαβάστε  παρ. 5.1-5.3 από το [2] (δεν εχουμε προλάβει να τελειώσουμε όλο το 5.3).
    • Φυλλάδιο 5 Αρχείο
      Οι φοιτητές πρέπει να
      Επισήμανση ως ολοκληρωμένου