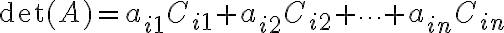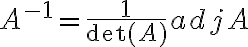10 Νοεμβρίου - 16 Νοεμβρίου
Section outline
-
Ορίσαμε την έννοια της ορίζουσας ενός
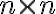 πίνακα
πίνακα 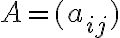 . Είδαμε ότι η ορίζουσα μπορεί να αναπτυχθεί ως προς οποιαδήποτε γραμμή και ισούται με
. Είδαμε ότι η ορίζουσα μπορεί να αναπτυχθεί ως προς οποιαδήποτε γραμμή και ισούται με όπου η παραπάνω σχέση είναι το ανάπτυγμα ως προς την γραμμή
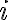 και
και 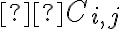 είναι ο i,j-συμπαράγοντας του Α. Δηλαδή
είναι ο i,j-συμπαράγοντας του Α. Δηλαδή 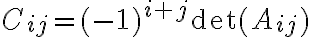 όπου
όπου 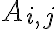 είναι ο
είναι ο 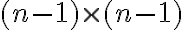 πίνακας που προκύπτει από τον A αν διαγράψουμε την i-γραμμή και τη j-στήλη. Είδαμε βασικές ιδιότητες της ορίζουσας:
πίνακας που προκύπτει από τον A αν διαγράψουμε την i-γραμμή και τη j-στήλη. Είδαμε βασικές ιδιότητες της ορίζουσας: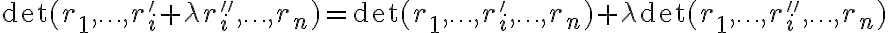
- Αν δύο γραμμές του Α είναι ίδιες τότε
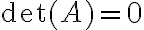
-
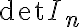 =1
=1 - Αν εναλλάξουμε δύο γραμμές του πίνακα η ορίζουσα αλλάζει πρόσημο
- Αν ο πίνακας B προκύπτει από τον πίνακα A προσθέτοντας στην γραμμή i ένα πολλαπλάσιο της γραμμής j, τότε η ορίζουσα παραμένει ίδια, δηλαδή
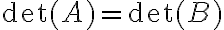
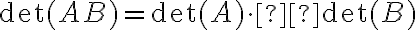
- Αν ο πίνακας A είναι άνω (ή κάτω) τριγωνικός, τότε η ορίζουσα του είναι ίση με το γινόμενο των στοιχείων της διαγωνίου.
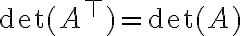 (και άρα μπορούμε να πάρουμε ανάπτυγμα ορίζουσας ως προς οποιαδήποτε στήλη και όχι μόνο γραμμή)
(και άρα μπορούμε να πάρουμε ανάπτυγμα ορίζουσας ως προς οποιαδήποτε στήλη και όχι μόνο γραμμή)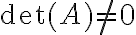 αν και μόνο αν Α είναι αντιστρέψιμος.
αν και μόνο αν Α είναι αντιστρέψιμος.
Κάναμε παραδείγματα υπολογισμού οριζουσών και είδαμε σαν εφαρμογή ότι μπορούμε να υπολογίσουμε τον αντίστροφο (αν υπάρχει) ενός πίνακα Α σαν
όπου
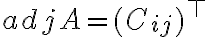 είναι ο ανάστροφος του πίνακα συμπαραγόντων του Α.
είναι ο ανάστροφος του πίνακα συμπαραγόντων του Α.Διαβάστε: παρ.2.3 από το [2]