27 Οκτωβρίου - 2 Νοεμβρίου
Section outline
-
Είδαμε ότι για κάθε γραμμική απεικόνιση
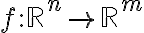 , υπάρχει ένας (μοναδικός) πίνακας
, υπάρχει ένας (μοναδικός) πίνακας 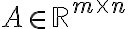 , τέτοιος ώστε
, τέτοιος ώστε 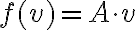 για κάθε
για κάθε 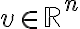 . Αυτός ο πίνακας ονομάζεται πίνακας της
. Αυτός ο πίνακας ονομάζεται πίνακας της  και τον συμβολίζουμε με
και τον συμβολίζουμε με ![[f] [f]](https://elearn.uoc.gr/filter/tex/pix.php/7b93cec8a8b3e110392556212941efcd.gif) .
. Είδαμε ότι μπορούμε να γενικεύσουμε τον παραπάνω ορισμό ως εξής: αν θεωρήσουμε μία βάση
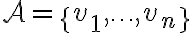 του
του  και μία βάση
και μία βάση 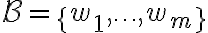 του
του 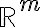 , τότε
, τότε Ο πίνακας
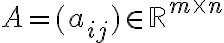 ονομάζεται πίνακας της
ονομάζεται πίνακας της  ως προς τις βάσεις
ως προς τις βάσεις 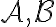 και τον συμβολίζουμε με
και τον συμβολίζουμε με ![[f]_{\mathcal{A}}^{\mathcal{B}} [f]_{\mathcal{A}}^{\mathcal{B}}](https://elearn.uoc.gr/filter/tex/pix.php/b06f260e0079d40e1b534a73ca3e3054.gif) . Ο πίνακας της
. Ο πίνακας της  είναι ο πίνακας ως προς τις κανονικές βάσεις,
είναι ο πίνακας ως προς τις κανονικές βάσεις, 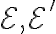 , των
, των  και
και 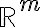 αντίστοιχα.
αντίστοιχα.Διαβάστε: παρ. 4.1 από το βιβλίο [2].