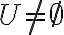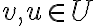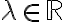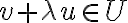Section outline

  • Είδαμε την έννοια του υπόχωρου ενός διανυσματικού χώρου. Ειδικότερα, δείξαμε ότι αν 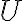U είναι ένα υποσύνολο του \mathbb{R}^n, τότε είναι υπόχωρος του \mathbb{R}^n αν 

    1. U\neq \emptyset,
    2. Για κάθε v, u\in U και κάθε \lambda \in \mathbb{R} ισχύει v+\lambda u\in U.

     

    Είδαμε παραδείματα.

    Αν 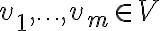v_1,\ldots,v_m\in V τότε ορίσαμε τον υπόχωρο που παράγεται από τα 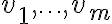v_1,\ldots, v_m ως το σύνολο 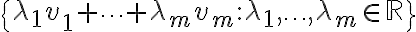\{\lambda_1 v_1 + \cdots + \lambda_m v_m : \lambda_1,\ldots,\lambda_m\in \mathbb{R}\} και το συμβολίσαμε με \langle v_1,\ldots,v_m\rangle.

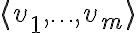    Είδαμε επίσης, ότι αν 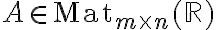A\in \mathrm{Mat}_{m\times n}(\mathbb{R}) τότε το σύνολο λύσεων του ομογενούς συστήματος 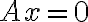A x = 0 είναι υπόχωρος του \mathbb{R}^n.

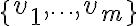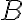    Ορίσαμε πότε ένα σύνολο διανυσμάτων \{v_1,\ldots,v_m\} είναι γραμμικώς εξαρτημένο/ανεξάρτητο και είδαμε παραδείγματα. Είδαμε πώς μπορούμε να εξετάζουμε (αλγοριθμικά) εάν ένα δεδομένο σύνολο είναι εξαρτημένο/ανεξάρτητο. Εάν V είναι ένας υπόχωρος του \mathbb{R}^n και B ένα σύνολο διανυσμάτων του, λέμε ότι το 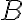B είναι βάση του V εάν:

    1. Παράγει τον V, δηλαδή V = \langle B\rangle και
    2. Είναι γραμμικώς ανεξάρτητο.

     

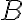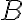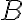    Είδαμε ότι η απαίτηση της γραμμικής ανεξαρτησίας του B εξασφαλίζει ότι κανένα γνήσιο υποσύνολο του B δεν παράγει τον V. Με άλλα λόγια κάθε διάνυσμα του B είναι απαραίτητο. 

    Διαβάστε: παρ. 3.2 από το βιβλίο [2].

    Διαβάστε: παρ. 3.3 έως τη σελ. 89 από το βιβλίο [2].